\(x+3+\sqrt{1-x^2}=3\sqrt{x+1}+\sqrt{1-x}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4) Ta có: \(\left(x+3\right)\cdot\sqrt{10-x^2}=x^2-x-12\)
\(\Leftrightarrow\left(x+3\right)\cdot\sqrt{10-x^2}-\left(x-4\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(\sqrt{10-x^2}-x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\\sqrt{10-x^2}=x-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\10-x^2=x^2-8x+16\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x^2-8x+16-10+x^2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\2x^2-8x+6=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\2\left(x^2-4x+3\right)=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\\left(x-1\right)\left(x-3\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=1\\x=3\end{matrix}\right.\)

\(\dfrac{15\sqrt{x}-11}{x+2\sqrt{x}-3}+\dfrac{3\sqrt{x}-2}{1-\sqrt{x}}-\dfrac{2\sqrt{x}+3}{\sqrt{x}+3}\)
\(=\dfrac{15\sqrt{x}-11}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}-\dfrac{\left(3\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}-\dfrac{\left(2\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{15\sqrt{x}-11-\left(3\sqrt{x}-2\right)\left(\sqrt{x}+3\right)-\left(2\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{15\sqrt{x}-11-3x-9\sqrt{x}+2\sqrt{x}+6-2x+2\sqrt{x}-3\sqrt{x}+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{-5x+7\sqrt{x}-2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{-\left(5x-7\sqrt{x}+2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{-\left(5\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=-\dfrac{5\sqrt{x}-2}{\sqrt{x}+3}\)
\(\dfrac{x\sqrt{x}+1}{\sqrt{x}+1}\) (ĐK: \(x\ge0\))
\(=\dfrac{\left(\sqrt{x}\right)^3+1^3}{\sqrt{x}+1}\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\sqrt{x}+1}\)
\(=x-\sqrt{x}+1\)
______________
\(\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+9}{x-9}\) (ĐK: \(x\ge0;x\ne9\))
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}+\dfrac{2\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{3x+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x-3\sqrt{x}+2x+6\sqrt{x}-3x-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{3\sqrt{x}-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{3\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{3}{\sqrt{x}+3}\)

từ dòng cuối là sai rồi bạn à
Bạn bỏ dòng cuối đi còn lại đúng rồi
Ở tử đặt nhân tử chung căn x chung rồi lại đặt căn x +1 chung
Ở mẫu tách 3 căn x ra 2 căn x +căn x rồi đặt nhân tử 2 căn x ra
rút gọn được \(\frac{3\sqrt{x}-5}{2\sqrt{x}+1}\)

1.
ĐKXĐ: \(x< 5\)
\(\Leftrightarrow\sqrt{\dfrac{42}{5-x}}-3+\sqrt{\dfrac{60}{7-x}}-3=0\)
\(\Leftrightarrow\dfrac{\dfrac{42}{5-x}-9}{\sqrt{\dfrac{42}{5-x}}+3}+\dfrac{\dfrac{60}{7-x}-9}{\sqrt{\dfrac{60}{7-x}}+3}=0\)
\(\Leftrightarrow\dfrac{9x-3}{\left(5-x\right)\left(\sqrt{\dfrac{42}{5-x}}+3\right)}+\dfrac{9x-3}{\left(7-x\right)\left(\sqrt{\dfrac{60}{7-x}}+3\right)}=0\)
\(\Leftrightarrow\left(9x-3\right)\left(\dfrac{1}{\left(5-x\right)\left(\sqrt{\dfrac{42}{5-x}}+3\right)}+\dfrac{1}{\left(7-x\right)\left(\sqrt{\dfrac{60}{7-x}}+3\right)}\right)=0\)
\(\Leftrightarrow x=\dfrac{1}{3}\)
b.
ĐKXĐ: \(x\ge2\)
\(\sqrt{\left(x-2\right)\left(x-1\right)}+\sqrt{x+3}=\sqrt{x-2}+\sqrt{\left(x-1\right)\left(x+3\right)}\)
\(\Leftrightarrow\sqrt{\left(x-2\right)\left(x-1\right)}-\sqrt{x-2}+\sqrt{x+3}-\sqrt{\left(x-1\right)\left(x+3\right)}=0\)
\(\Leftrightarrow\sqrt{x-2}\left(\sqrt{x-1}-1\right)-\sqrt{x+3}\left(\sqrt{x-1}-1\right)=0\)
\(\Leftrightarrow\left(\sqrt{x-1}-1\right)\left(\sqrt{x-2}-\sqrt{x+3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-1}-1=0\\\sqrt{x-2}-\sqrt{x+3}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=1\\x-2=x+3\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow x=2\)

1) \(\dfrac{1}{\sqrt{3}+1}+\dfrac{1}{\sqrt{3}-1}-2\sqrt{3}=\dfrac{\sqrt{3}-1+\sqrt{3}+1}{3-1}-2\sqrt{3}=\sqrt{3}-2\sqrt{3}=-\sqrt{3}\)
+) \(ĐKXĐ:\left\{{}\begin{matrix}x>0\\x\ne1\\x\ne4\end{matrix}\right.\)
\(P=\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}}\right):\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\right)\)
\(P=\dfrac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{x-1-x+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\)
\(P=\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}{3}\)
\(P=\dfrac{\sqrt{x}-2}{3\sqrt{x}}\)
2) \(\sqrt{3-2\sqrt{2}}+\dfrac{1}{\sqrt{2}-1}=\sqrt{2}-1+\sqrt{2}+1=2\sqrt{2}\)
+) \(ĐKXĐ:\left\{{}\begin{matrix}a>0\\a\ne4\end{matrix}\right.\)
\(M=\left(\dfrac{\sqrt{a}}{\sqrt{a}-2}+\dfrac{\sqrt{a}}{\sqrt{a}+2}\right)\cdot\dfrac{a-4}{\sqrt{4a}}\)
\(M=\dfrac{a+2\sqrt{a}+a-2\sqrt{a}}{a-4}\cdot\dfrac{a-4}{2\sqrt{a}}\)
\(M=\dfrac{2a}{2\sqrt{a}}=\sqrt{a}\)
+) \(ĐKXĐ:\left\{{}\begin{matrix}x\ge0\\x\ne4\end{matrix}\right.\)
\(N=\left(1-\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\left(\dfrac{\sqrt{x}+2}{\sqrt{x}+3}+\dfrac{\sqrt{x}-3}{2-\sqrt{x}}+\dfrac{\sqrt{x}-2}{x+\sqrt{x}-6}\right)\)
\(N=\dfrac{\sqrt{x}+1-\sqrt{x}}{\sqrt{x}+1}:\left(\dfrac{\sqrt{x}+2}{\sqrt{x}+3}-\dfrac{\sqrt{x}-3}{\sqrt{x}-2}+\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\right)\)
\(N=\dfrac{1}{\sqrt{x}+1}:\dfrac{x-4-x+9+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\)
\(N=\dfrac{1}{\sqrt{x}+1}\cdot\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}{\sqrt{x}+3}\)
\(N=\dfrac{\sqrt{x}-2}{\sqrt{x}+1}\)
+) \(ĐKXĐ:\left\{{}\begin{matrix}x\ge0\\x\ne9\\x\ne4\end{matrix}\right.\)
\(Q=\left(1-\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\left(\dfrac{\sqrt{x}+2}{\sqrt{x}-3}+\dfrac{\sqrt{x}-8}{x-5\sqrt{x}+6}+\dfrac{\sqrt{x}+3}{2-\sqrt{x}}\right)\)
\(Q=\dfrac{\sqrt{x}+1-\sqrt{x}}{\sqrt{x}+1}:\left(\dfrac{\sqrt{x}+2}{\sqrt{x}-3}+\dfrac{\sqrt{x}-8}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\right)\)
\(Q=\dfrac{1}{\sqrt{x}+1}:\dfrac{x-4+\sqrt{x}-8-x+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(Q=\dfrac{1}{\sqrt{x}+1}\cdot\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}{\sqrt{x}-3}\)
\(Q=\dfrac{\sqrt{x}-2}{\sqrt{x}+1}\)
p/s: sorry tại n' câu wa nên mình ko làm chi tiết đc =(( lần sau nhớ chia các câu ra cho dễ nhìn hơn nha, đánh hơi mỏi tay :'( có j ko hỉu cmt dưới nha

4 , Ta có :
\(\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x-9}{x-9}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{x-9}+\dfrac{2\sqrt{x}\left(\sqrt{x}+3\right)}{x-9}-\dfrac{3\left(x-3\right)}{x-9}\)
\(=\dfrac{x-3\sqrt{x}+2x+6\sqrt{x}-3x+9}{x-9}\)
\(=\dfrac{3\sqrt{x}+9}{x-9}\)
\(=\dfrac{3\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{3}{\sqrt{x}-3}\)
2 , Ta có :
\(\dfrac{x\sqrt{x}+1}{x-1}-\dfrac{x-1}{\sqrt{x}+1}=\dfrac{x\sqrt{x}+1}{x-1}-\dfrac{\left(x-1\right)\left(\sqrt{x}-1\right)}{x-1}\)
\(=\dfrac{x\sqrt{x}+1}{x-1}-\dfrac{x\sqrt{x}-x-\sqrt{x}+1}{x-1}\)
\(=\dfrac{x\sqrt{x}+1-x\sqrt{x}+x+\sqrt{x}-1}{x-1}=\dfrac{\sqrt{x}}{\sqrt{x}-1}\)

2. \(\dfrac{\sqrt{x^2}-16}{\sqrt{x-3}}+\sqrt{x+3}=\dfrac{7}{\sqrt{x-3}}\) (2)
\(\Leftrightarrow\dfrac{\sqrt{x^2}-16}{\sqrt{x-3}}+\sqrt{x+3}-\dfrac{7}{\sqrt{x-3}}=0\)
\(\Leftrightarrow\dfrac{\sqrt{x^2}-16+\sqrt{\left(x-3\right)\left(x+3\right)}-7}{\sqrt{x-3}}=0\)
\(\Leftrightarrow\sqrt{x^2}-16+\sqrt{\left(x-3\right)\left(x+3\right)}-7=0\)
\(\Leftrightarrow\left|x\right|-16+\sqrt{x^2-9}-7=0\)
\(\Leftrightarrow\left|x\right|-23+\sqrt{x^2-9}=0\)
\(\Leftrightarrow\sqrt{x^2-9}=-\left|x\right|+23\)
\(\Leftrightarrow x^2-9=-\left(-\left|x\right|+23\right)^2\)
\(\Leftrightarrow x^2-9=-\left(-\left|x\right|\right)^2-46\cdot\left|x\right|+529\)
\(\Leftrightarrow x^2-9=\left|x\right|^2-46+\left|x\right|+529\)
\(\Leftrightarrow x^2-9=x^2-46\cdot\left|x\right|+529\)
\(\Leftrightarrow-9=-46\cdot\left|x\right|+529\)
\(\Leftrightarrow46\cdot\left|x\right|=529+9\)
\(\Leftrightarrow49\cdot\left|x\right|=538\)
\(\Leftrightarrow\left|x\right|=\dfrac{269}{23}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{269}{23}\\x=-\dfrac{269}{23}\end{matrix}\right.\)
Sau khi dùng phép thử ta nhận thấy \(x\ne-\dfrac{269}{23}\)
Vậy tập nghiệm phương trình (1) là \(S=\left\{\dfrac{269}{23}\right\}\)
3. sửa đề: \(\sqrt{14-x}=\sqrt{x-4}\sqrt{x-1}\) (3)
\(\Leftrightarrow\sqrt{14-x}=\sqrt{\left(x-4\right)\left(x-1\right)}\)
\(\Leftrightarrow\sqrt{14-x}=\sqrt{x^2-x-4x+4}\)
\(\Leftrightarrow\sqrt{14-x}=\sqrt{x^2-5x+4}\)
\(\Leftrightarrow14-x=x^2-5x+4\)
\(\Leftrightarrow14-x-x^2+5x-4=0\)
\(\Leftrightarrow10+4x-x^2=0\)
\(\Leftrightarrow-x^2+4x+10=0\)
\(\Leftrightarrow x^2-4x-10=0\)
\(\Leftrightarrow x=\dfrac{-\left(-4\right)\pm\sqrt{\left(-4\right)^2-4\cdot1\cdot\left(-10\right)}}{2\cdot1}\)
\(\Leftrightarrow x=\dfrac{4\pm\sqrt{16+40}}{2}\)
\(\Leftrightarrow x=\dfrac{4\pm\sqrt{56}}{2}\)
\(\Leftrightarrow x=\dfrac{4\pm2\sqrt{14}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{4-2\sqrt{14}}{2}\\x=\dfrac{4+2\sqrt{14}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2+\sqrt{14}\\x=2-\sqrt{14}\end{matrix}\right.\)
sau khi dùng phép thử ta nhận thấy \(x\ne2-\sqrt{14}\)
Vậy tập nghiệm phương trình (3) là \(S=\left\{2+\sqrt{14}\right\}\)

1: \(\Leftrightarrow\dfrac{3x-1}{x+2}=4\)
=>4x+8=3x-1
=>x=-9
2: \(\Leftrightarrow\dfrac{5x-7}{2x-1}=4\)
=>8x-4=5x-7
=>3x=-3
=>x=-1
3: ĐKXD: x>=0
\(PT\Leftrightarrow\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)=\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)\)
=>\(x+\sqrt{x}-6=x-1\)
=>căn x=-1+6=5
=>x=25
4: ĐKXĐ: x>=0
PT =>\(\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)=\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)\)
=>x-2*căn x-3=x-4
=>-2căn x-3=-4
=>2căn x+3=4
=>2căn x=1
=>căn x=1/2
=>x=1/4

\(\left(\dfrac{1}{\sqrt{x}}-\sqrt{x}\right):\left(\dfrac{1-\sqrt{x}}{x+\sqrt{x}}\right)\) (ĐK: \(x>0\))
\(=\left(\dfrac{1}{\sqrt{x}}-\dfrac{x}{\sqrt{x}}\right)\cdot\dfrac{-\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}-1}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{-\sqrt{x}}\cdot\dfrac{-\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}-1}\)
\(=\dfrac{-\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}{-\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(=\left(\sqrt{x}+1\right)^2\)
c: 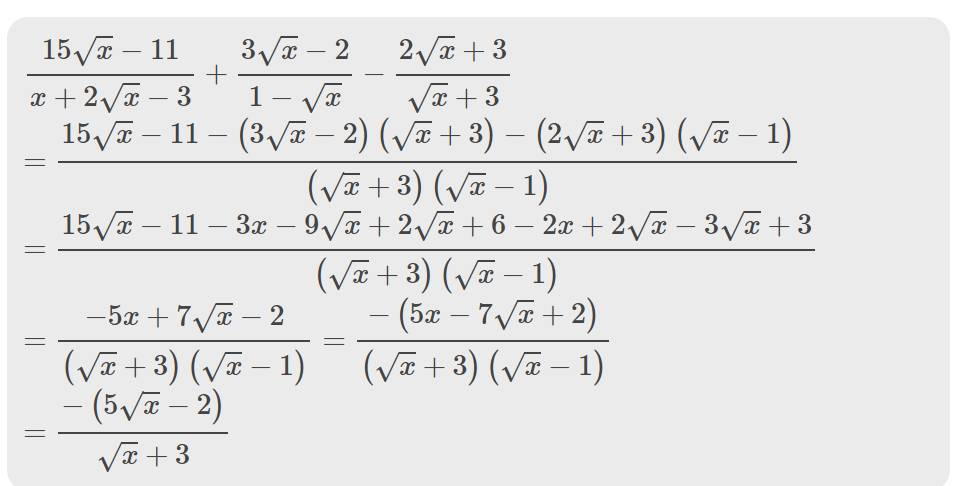
b;
Sửa đề: \(\dfrac{x\sqrt{x}+26\sqrt{x}-19}{x+2\sqrt{x}-3}-\dfrac{2\sqrt{x}}{\sqrt{x}-1}+\dfrac{\sqrt{x}-3}{\sqrt{x}+3}\)\(=\dfrac{x\sqrt{x}+26\sqrt{x}-19-2\sqrt{x}\left(\sqrt{x}+3\right)+\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x\sqrt{x}+26\sqrt{x}-19-2x-6\sqrt{x}+x-4\sqrt{x}+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x\sqrt{x}-x+16\sqrt{x}-16}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}=\dfrac{x+16}{\sqrt{x}+3}\)
Đặt \(\hept{\begin{cases}\sqrt{x-1}=a\\\sqrt{x+1}=b\end{cases}\left(a;b>0\right)\Rightarrow}b^2-a^2=0\)
\(b^2+2+ab=3b+a\)
\(\Leftrightarrow a\left(b-1\right)+\left(b^2-2b+1\right)-\left(b-1\right)=0\)
\(\Leftrightarrow a\left(b-1\right)+\left(b-1\right)^2-\left(b-1\right)=0\)
\(\Leftrightarrow\left(b-1\right)\left(a+b-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}b=1\\a+b=2\end{cases}}\)
Tự làm nốt nhé~~~