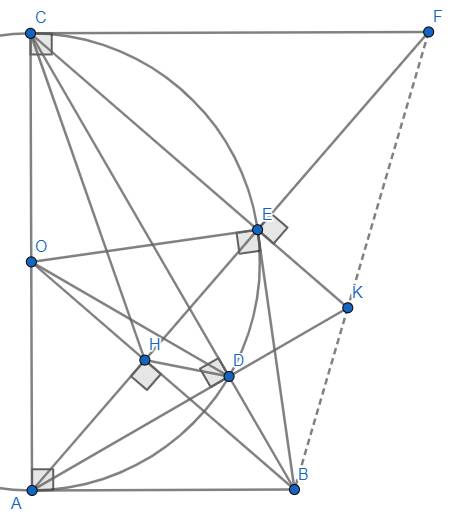
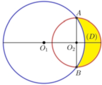
Cho tam giác ABC vuông tại a . Vẽ nửa đường tròn O1 đường kính AB. Nửa đường tròn O2 đường kính AC.Một đường thẳng D quay quanh A cắt đường tròn O1 tại D , O2 tại E.
CMR
Trung điểm DE luôn thuộc đường tròn cố định
Xác định vị trí đường tròn DE sao cho SBDEC lớn nhất