cho đoạn AB và hai điểm E ,K thuộc đoạn AB sao cho AE =BK . chứng minh rằng AB và EK có cùng trung điểm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) A---------E--------------------M--------------------K----------B
Gọi M là trung điểm của AB => AM =BM = AB/2
Vì AE = BK
+ Nếu AE < AM như hình vé => AM -AE = MB - BK => EM = MK => M là trung điểm của EK
+ Nếu AE > AM tự vẽ hình
=> AE - AM = BK - MB => EM = E=MK => M là trung điểm của EK
Vậy AB;EK có chung trung điểm là M
2) 4 đường thẳng ( phân biệt hay ko ?)
3) n(n-1):2 =105 => n(n-1) =210 =15.14
=> n = 15

Trường hợp :
Gọi M là trung điểm của AB. Khi đó MA = MB = a.
Điểm E nằm giữa hai điểm A và M, điểm F nằm giữa hai điểm B và M.
Do đó ME = MA - AE = a - AE; MF = MB - BF = a - BF.
Vì AE = BF nên ME = MF. Vậy M là trung điểm chung của hai đoạn thẳng AB và EF. Qua M vẽ thì xy là đường trung trực chung của AB và EF.
Trường hợp : Chứng minh tương tự

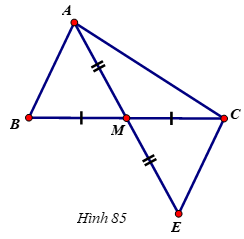
a: Xét ΔAMB và ΔEMC có
MA=ME
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔAMB=ΔEMC
b: Ta có: ΔAMB=ΔEMC
=>AB=CE
Ta có: ΔAMB=ΔEMC
=>\(\widehat{MAB}=\widehat{MEC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//EC
c: Xét ΔHAM và ΔKEM có
HA=KE
\(\widehat{HAM}=\widehat{KEM}\)
AM=EM
Do đó: ΔHAM=ΔKEM
=>\(\widehat{AMH}=\widehat{EMK}\)
mà \(\widehat{AMH}+\widehat{HME}=180^0\)(hai góc kề bù)
nên \(\widehat{EMK}+\widehat{HME}=180^0\)
=>H,M,E thẳng hàng

1 , vì M là trung điểm của AB nên
AM=BM=8:2=4(cm)
ta có:BD+MD=BM
\(\Rightarrow\)3+MD=4
\(\Rightarrow\)MD=1(cm)
ta có:AC+MC=AM
\(\Rightarrow\)3+CM=4
\(\Rightarrow\)CM=1(cm)
mà CD=CM+MD=1+1=2(cm)
b,vì CM+MD=CD:2
\(\Rightarrow\)suy ra M là trung điểmCD