: Tìm cặp giá trị (x;y) thỏa mãn \(\hept{\begin{cases}x^4+2y^3-x=-\frac{1}{4}+3\sqrt{3}\\y^4+2x^3-y=-\frac{1}{4}-3\sqrt{3}\end{cases}.}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: x – y – 3 = 0 ⇔ x – y = 3
Có vô số giá trị của x và y để biểu thức trên xảy ra
Các cặp giá trị có dạng (x ∈R, y = x – 3)
Chẳng hạn: (x = 0; y = -3); (x = 1; y = -2)

Ta chỉ cần tìm hai phân thức là nghịch đảo của nhau.
Ví dụ: 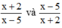 . Có vô số cặp phân thức như vậy.
. Có vô số cặp phân thức như vậy.
Có vô số cặp phân thức như vậy.

Ta có: 2x + y – 1 = 0 ⇔ 2x + y = 1
Có vô số giá trị của x và y để biểu thức trên xảy ra
Các cặp giá trị có dạng (x ∈R, y = 1 – 2x)
Chẳng hạn: (x = 0; y = 1); (x = 1; y = -1)


Các bạn xem mình làm thế này có đúng không:
Chỉ việc chọn hai phân thức nghịch đảo nhau với tử và mẫu đều chứ biến X và không có giá trị nào của X để tử và mẫu đồng thời bằng 0. Chẳn hạn:
\(\frac{x-1}{x+1}and\frac{x+1}{x-1}\)
Vậy: Có vô số cặp phân thức như thế.



Nhận xét : Nếu cộng các đẳng thức, ta nhận được:
\(\left(x^4+2x^3-x+\frac{1}{4}\right)+\left(y^4+2y^3-y+\frac{1}{4}\right)=0.\)
Với việc chọn đa thức \(P\left(x\right)=\left(x-a\right)^2\left(x-b\right)^2,\)sau khi khai triển và đồng nhất hệ số với đa thức \(Q\left(x\right)=x^4+2x^3-x+\frac{1}{4}\)ta được: \(a=\frac{-1+\sqrt{3}}{2}\)và \(b=\frac{-1-\sqrt{3}}{2}.\)
Lời giải: Xét đa thức: \(P\left(x\right)=\left(x-\frac{-1+\sqrt{3}}{2}\right)^2\left(x-\frac{-1-\sqrt{3}}{2}\right)^2,\)
Thấy rằng với mọi \(x\in R\)thì \(P\left(x\right)\)luôn không âm. Suy ra
\(0\le P\left(x\right)+P\left(y\right)=\left(x+2x^3-x+\frac{1}{4}\right)+\left(y^4+2y^3-y+\frac{1}{4}\right)\)
\(=\left(x^4+2y^3-x\right)+\left(y^4+2x^3-y\right)+\frac{1}{4}+\frac{1}{4}\)
\(=-\frac{1}{4}+3\sqrt{3}+\left(-\frac{1}{4}-3\sqrt{3}\right)+\frac{1}{4}+\frac{1}{4}\)
\(=0\)
Vì \(P\left(x\right);P\left(y\right)\)đều không âm nên dấu '=' xảy ra khi và chỉ khi \(P\left(x\right)=P\left(y\right)=0\).
Do đó: \(x,y\in\left\{\frac{-1+\sqrt{3}}{2};\frac{-1-\sqrt{3}}{2}\right\}.\)Thay vào phương trình và dùng phép thử trực tiếp, ta thu nhận được:
\(x=\frac{-1-\sqrt{3}}{2},y=\frac{-1+\sqrt{3}}{2}.\)