Giải pt:
x4=3x2+10x+4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 1 2022
a) \(=6x^3+8x^2+2x-6x^3=8x^2+2x\)
b) \(=\left[3xy\left(xy+2xy^2-4\right)\right]:3xy=xy+2xy^2-4\)
c) \(=\dfrac{10x}{\left(x-2\right)\left(x+2\right)}+\dfrac{3}{x+2}-\dfrac{5}{x-2}=\dfrac{10x+3\left(x-2\right)-5\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{8x-16}{\left(x-2\right)\left(x+2\right)}=\dfrac{8\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{8}{x+2}\)
DT
10 tháng 1 2022
a, \(=6x^3+12x^2+2x-6x^3\\=12x^2+2x\)
b,
\(=xy+2xy^2-4\)
c,
\(\dfrac{10x}{x^2-4}+\dfrac{3}{x+2}-\dfrac{5}{x-2}\)
\(=\dfrac{10x}{\left(x-2\right)\left(x+2\right)}+\dfrac{3x-6}{\left(x-2\right)\left(x+2\right)}-\dfrac{5x+10}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{10x+3x-6-5x-10}{\left(x-2\right)\left(x+2\right)}=\dfrac{8x-16}{\left(x-2\right)\left(x+2\right)}=\dfrac{8\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{8}{x+2}\)
CM
26 tháng 10 2017
Đáp án C.
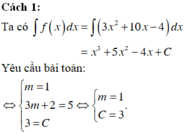
Vậy m = 1 là giá trị cần tìm thỏa mãn yêu cầu bài toán
Cách 2:
Ta có F ' x = m x 2 + 3 m + 2 x 2 − 4 x + 3 ' = 3 m x 2 + 2 3 m + 2 x − 4.
Vì F(x) là một nguyên hàm của f(x) nên ta có F ' x = f x , ∀ x .
Do đó 3 m x 2 + 2 3 m + 2 x − 4 = 3 x 2 + 10 x − 4 .
Đồng nhất hệ số hai vế ta có
m = 1 2 3 m + 2 = 10 ⇔ m = 1 .
CM
20 tháng 9 2017
Chọn A.
∫ 3 x 2 + 10 x - 4 d x = x 3 + 5 x 2 - 4 x + C , nên m = 1.