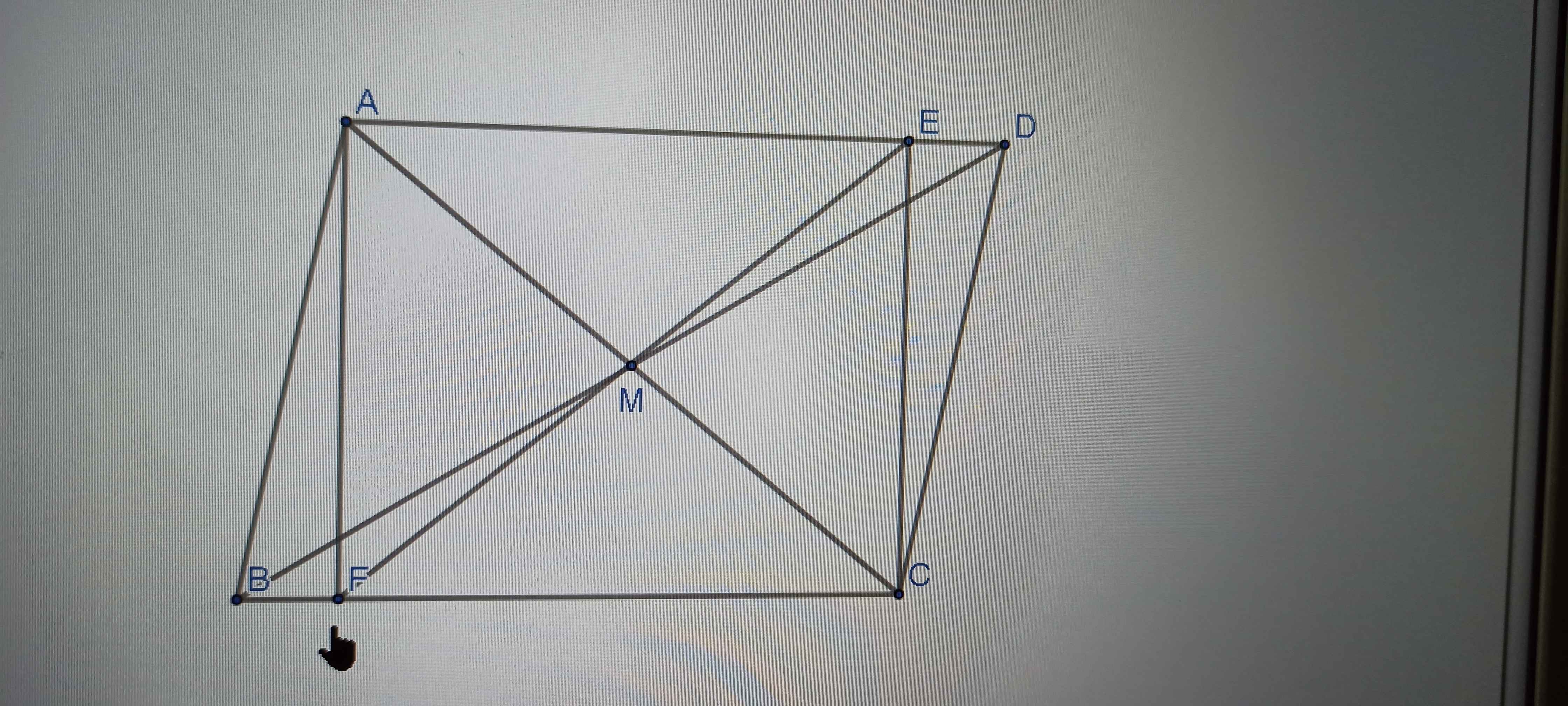
Cho tam giác ABC cân tại A. Trên tia đối của AB lấy điểm D, trên tia đối của tia AC lấy điểm E sao cho AD = AE. Chứng minh:
a) BE = CD
b) DE // BC
c) tam giác BED = tam giác CED
d) Gọi M là trung điểm của BC. Chứng minh rằng AM vuông góc DE
AI GIẢI NHANH VÀ ĐÚNG MIK SẼ TICK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

10 tháng 7 2019
Tham khảo :
Câu hỏi của nguyen thi thom - Toán lớp 7 - Học toán với OnlineMath
Học tốt!!!
KN
10 tháng 7 2019
Câu hỏi của Chi Chi - Toán lớp 7 - Học toán với OnlineMath
Tham khảo tại link trên.

16 tháng 7 2021
Câu C bạn cm AFCE là hình chữ nhật , FE là đường chéo => E,F,M thẳng hàng vì 2 đường chéo hình chữ nhật đi qua trung điểm của mỗi đường.

12 tháng 10 2021
a: Xét ΔABC và ΔAED có
AB=AE
\(\widehat{BAC}=\widehat{EAD}\)
AC=AD
Do đó: ΔABC=ΔAED

a) Xét \(\Delta EAB\)và \(\Delta DAC\)có:
\(AE=AD\)(gt)
\(\widehat{EAB}=\widehat{DAC}\)(đối đỉnh)
\(AB=AC\)(Do tam giác ABC cân tại A)
Suy ra \(\Delta EAB=\Delta DAC\left(c.g.c\right)\)
\(\Rightarrow BE=CD\)(hai cạnh tương ứng)