Phương trình : \(sin5x-sinx=0\) có bao nhiêu nghiệm thuộc đoạn \(\left[-2018\Pi;2018\Pi\right]\) ?
A . 20179
B . 20181
C . 16144
D . 16145
Trình bày bài giải chi tiết rồi ms chọn đáp án nha các bạn .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 9 2023
=>2cos2x=pi(loại) hoặc sin x-cosx=0
=>sin x-cosx=0
=>sin(x-pi/4)=0
=>x-pi/4=kpi
=>x=kpi+pi/4
mà x\(\in\left[-pi;pi\right]\)
nên \(x\in\left\{\dfrac{pi}{4};-\dfrac{3}{4}pi\right\}\)
=> D
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 12 2020
\(\Leftrightarrow2\left(cos^2x-sin^2x\right)+sinx.cosx\left(sinx+cosx\right)=m\left(sinx+cosx\right)\)
\(\Leftrightarrow\left(2cosx-2sinx\right)\left(sinx+cosx\right)+sinx.cosx\left(sinx+cosx\right)=m\left(sinx+cosx\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=0\left(\text{vô nghiệm trên đoạn xét}\right)\\2cosx-2sinx+sinx.cosx=m\left(1\right)\end{matrix}\right.\)
Xét (1), đặt \(t=cosx-sinx=\sqrt{2}cos\left(x+\dfrac{\pi}{4}\right)\)
\(\Rightarrow\left\{{}\begin{matrix}t\in\left[-1;1\right]\\sinx.cosx=\dfrac{1-t^2}{2}\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow2t+\dfrac{1-t^2}{2}=m\)
Xét hàm \(f\left(t\right)=-\dfrac{1}{2}t^2+2t+\dfrac{1}{2}\) trên \(\left[-1;1\right]\)
\(-\dfrac{b}{2a}=2\notin\left[-1;1\right]\) ; \(f\left(-1\right)=-2\) ; \(f\left(1\right)=2\)
\(\Rightarrow-2\le f\left(t\right)\le2\Rightarrow-2\le m\le2\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 9 2021
\(0< \dfrac{1}{2018}< 1\)
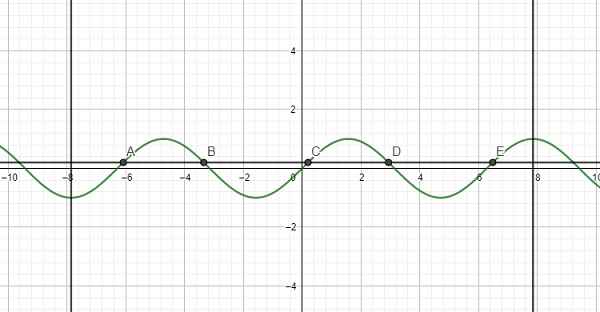
Kẻ 1 đường thẳng nằm ngang nằm giữa \(y=0\) và \(y=1\) ta thấy cắt đồ thị tại 5 điểm trên đoạn đã cho
\(\Rightarrow\) Pt có 5 nghiệm
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 8 2021
\(cos\left(\dfrac{\pi}{6}-2x\right)=cos\left(\dfrac{\pi}{2}-x\right)\)
\(\Rightarrow\left[{}\begin{matrix}\dfrac{\pi}{6}-2x=\dfrac{\pi}{2}-x+k2\pi\\\dfrac{\pi}{6}-2x=x-\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{3}+k2\pi\\x=\dfrac{2\pi}{9}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
\(\Rightarrow x=\left\{\dfrac{8\pi}{9};\dfrac{14\pi}{9};\dfrac{5\pi}{3}\right\}\) có 3 nghiệm
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 9 2021
Từ đường tròn lượng giác, trên \(\left(-\dfrac{\pi}{2};3\pi\right)\):
- Nếu \(0< t< 1\) thì \(sinx=t\) có 4 nghiệm
- Nếu \(-1< t< 0\) thì \(sinx=t\) có 3 nghiệm
- Nếu \(t=0\) thì \(sinx=t\) có 3 nghiệm
- Nếu \(t=1\) thì \(sinx=t\) có 2 nghiệm
- Nếu \(t=-1\) thì \(sinx=t\) có 1 nghiệm
Do đó pt đã cho có 5 nghiệm pb trong khoảng đã cho khi:
\(2t^2-\left(5m+1\right)t+2m^2+2m=0\) có 2 nghiệm pb thỏa mãn:
- TH1: \(\left\{{}\begin{matrix}t_1=-1\\0< t_2< 1\end{matrix}\right.\)
- TH2: \(\left\{{}\begin{matrix}-1< 0< t_1\\t_2=1\end{matrix}\right.\)
- TH3: \(\left\{{}\begin{matrix}t_1=0\\t_2=1\end{matrix}\right.\)
Về cơ bản, chỉ cần thay 1 nghiệm bằng 0 hoặc 1 rồi kiểm tra nghiệm còn lại có thỏa hay ko là được
17 tháng 9 2021
Em làm cách khác cơ.
Δ = (...)2 nên viết hẳn 2 nghiệm ra
rồi vẽ bảng biến thiên của y = sinx