giải PT :
2 cos2x + 3cosx - 2cos3x = 4sinx.sin3x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 10 2020
1.
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(\left(m+1\right)^2+\left(-3\right)^2\ge m^2\)
\(\Leftrightarrow...\)
2.
\(\Leftrightarrow3\left(\frac{1}{2}-\frac{1}{2}cos2x\right)+4m.sin2x-4=0\)
\(\Leftrightarrow8m.sin2x-3cos2x=5\)
Pt vô nghiệm khi: \(\left(8m\right)^2+\left(-3\right)^2< 5^2\)
\(\Leftrightarrow...\)
LT
1
KR
3 tháng 8 2019
cos2x = 1- sin^x
sin2x= 2sinxcosx
Nhóm lại bình thường và giải thôi
CM
6 tháng 12 2017
Chọn D
Bảng biến thiên
Dựa vào bảng biến thiên suy ra phương trình có nghiệm khi
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 10 2020
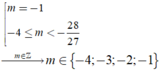
1.
ĐKXĐ: \(sin\left(2x+\frac{\pi}{7}\right)\ne0\)
\(\Leftrightarrow2x+\frac{\pi}{7}\ne k\pi\)
\(\Leftrightarrow...\)
2.
\(\Leftrightarrow1-cos2x+m.sin2x=2m\)
\(\Leftrightarrow m.sin2x-cos2x=2m-1\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất, pt vô nghiệm khi:
\(m^2+\left(-1\right)^2< \left(2m-1\right)^2\)
\(\Leftrightarrow...\)
3.
a.
\(\Leftrightarrow\left[{}\begin{matrix}sinx=-\frac{1}{2}\Leftrightarrow...\\cos2x+2sin2x=10\left(1\right)\end{matrix}\right.\)
Xét (1), ta có \(1^2+2^2< 10^2\) nên (1) vô nghiệm
b.
\(3cosx+2cos^2x-1-\left(4cos^3x-3cosx\right)+1=4sin^2x.cosx\)
\(\Leftrightarrow6cosx+2cos^2x-4cos^3x=4cosx\left(1-cos^2x\right)\)
\(\Leftrightarrow6cosx+2cos^2x-4cos^3x=4cosx-4cos^3x\)
\(\Leftrightarrow2cos^2x+2cosx=0\)
\(\Leftrightarrow cosx\left(cosx+1\right)=0\)
Vế phải là \(4sinx.sin3x\) hay \(4sinx.sin2x\) bạn?
Sin3x nhé cậu