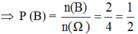Có 13 tấm bìa mỗi tấm bìa ghi một chữ số và xếp theo thứ tự như sau :
[1] [2] [3] [4] [5] [6] [7] [8] [9] [1] [2] [3] [4]
Không thay đổi thứ tự các tấm bìa, hãy đặt giữa chúng các phép tính +,-,*, và các dấu ngoặc nếu cần sao cho kết quả bẳng 2002
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài toán có rất nhiều cách đặt dấu phép tính và dấu ngoặc. Ví dụ:
Cách 1: (123 + 4 x 5) x (6 + 7 - 8 + 9 + 1 - 2 - 3 + 4) = 2002
Cách 2: (1 x 2 + 3 x 4) x (5 + 6) x [(7 + 8 + 9) - (1 + 2 x 3 + 4)] = 2002
Cách 3: (1 + 2 + 3 + 4 x 5) x (6 x 7 + 8 + 9 - 1 + 23 - 4) = 2002

+) Nhận xét: Mỗi số trong 671 số lẻ đã cho được viết 2 lần nên tổng của 671 số thu được gấp 2 lần tổng của 671 số lẻ đã cho
=> Tổng đó là số chẵn (*)
+) Nếu 671 số thu được đều là số lẻ => Tổng của 671 số lẻ là 1 số lẻ => Mâu thuẫn với (*)
=> Trong 671 số thu được có ít nhất 1 số chẵn
=> Tích của 671 số đó là chẵn

a) Mỗi phần tử của không gian mẫu là một tổ hợp chập 3 của 4 phần tử. Do đó, số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_4^3\) ( phần tử)
b) +) Sự kiện “Tổng các số trên ba tấm bìa bằng 9” tương ứng với biến cố \(A = \left\{ {\left( {4;3;2} \right)} \right\}\)
+) Sự kiện “Các số trên ba tấm bìa là ba số tự nhiên liên tiếp” tương ứng với biến cố \(B = \left\{ {\left( {1;2;3} \right),\left( {2;3;4} \right)} \right\}\)
c) +) Ta có: \(n\left( A \right) = 1\),\(n\left( B \right) = 2\)
+) Vậy xác suất của biến cố A và B là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{1}{4};P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega \right)}} = \frac{2}{4} = \frac{1}{2}\)

a.Không gian mẫu gồm 4 phần tử:
Ω = {(1, 2, 3);(1,2,4);(2,3,4);(1,3,4)} ⇒ n(Ω)=4
b.Các biến cố:
+ A = {1, 3, 4} ⇒ n(A) = 1
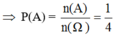
+ B = {(1, 2, 3), (2, 3, 4)} ⇒ n(B) = 2