Xét tính chẵn lẻ của hàm số: y=ax+b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


#)Bạn tham khảo nhé :
https://www.nguyentheanh.org/ly-thuyet-va-bai-tap-ve-ham-bac-hai-y-ax2-bx-c-a-%E2%89%A0-0-toan-lop-10/
P/s : Mình k hiểu rõ mấy về toán lớp 10 nhưng được thì bạn cứ tham khảo nhé ^^
Xét tính chẵn lẻ của hàm số: y=ax2 + bx + c
Bạn tham Khảo :
BL


Đặt `y=f(x)=x-sinx`
Có: `f(-x)=-x-sin(-x)=-x+sinx=-(x-sinx)=-f(x)`
`=>` Hàm lẻ.

y = √x
TXĐ: D = [0; +∞) ⇒ x ∈ D thì -x ∉ D
Vậy hàm số trên không là hàm số chẵn cũng không là hàm số lẻ.

Tập xác định D = R và ∀ x ∈ D có -x ∈ D và f(-x) = -2 = f(x)
Hàm số là hàm số chẵn

TXĐ: D=R
\(y\left(-x\right)=\left(-x\right)^3-5\left(-x\right)=-x^3+5x=-\left(x^3-5x\right)=-y\left(x\right)\)
\(\Rightarrow\) Hàm lẻ

y = f(x) = 3x2 – 2
TXĐ:D = R ⇒ x ∈ D thì-x ∈ D
Ta có: f(-x) = 3(-x)2 – 2 = 3x2 – 2 = f(x)
Vậy hàm số y = f(x) = 3x2 – 2 là hàm số chẵn

y = f(x) = 1/x
TXĐ: D = R \{0} ⇒ x ∈ D thì-x ∈ D
f(-x) = 1/(-x) = -1/x = -f(x)
Vậy y = f(x) = 1/x là hàm số lẻ.

Tập xác định D = R; ∀ x ∈ D có -x ∈ D và
f ( - x ) = 3 . ( - x ) 2 - 1 = 3 x 2 - 1 = f ( x )
Vậy hàm số đã cho là hàm số chẵn.
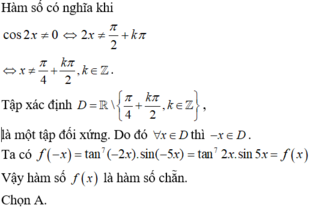
1. Khái niệm hàm số chẵn, hàm số lẻ
Cho hàm số y=f(x) có tập xác định D.
• Hàm số f được gọi là hàm số chẵn nếu với ∀x∈D thì −x∈D và f(x)=f(−x)
• Hàm số f được gọi là hàm số lẻ nếu với ∀x∈D thì −x∈D và f(x)=−f(−x)
Chú ý: Một hàm số có thể không chẵn cũng không lẻ.
2. Đồ thị của hàm số chẵn, hàm số lẻ
• Đồ thị của hàm số chẵn nhận trục tung làm trục đối xứng.
• Đồ thị của hàm số lẻ nhận gốc toạ độ làm tâm đối xứng.
3. Phương pháp xét tính chẵn, lẻ của hàm số
Cho hàm số y=f(x)y=f(x) xác định trên DD
• f là hàm số chẵn ⇔{∀x∈D⇒−x∈Df(−x)=f(x)
• f là hàm số lẻ ⇔{∀x∈D⇒−x∈Df(−x)=−f(x)
Các bước xét tính chẵn, lẻ của hàm số:
• Bước 1. Tìm tập xác định DD của hàm số.
• Bước 2. Kiểm tra:
+ Nếu ∀x∈D⇒−x∈D∀x∈D⇒−x∈D thì chuyển qua bước 3.
+ Nếu tồn tại x0∈Dx0∈D mà −x0∉D−x0∉D thì kết luận hàm không chẵn cũng không lẻ.
• Bước 3. Xác định f(−x)f(−x) và so sánh với f(x):f(x):
+ Nếu f(−x)=f(x) thì kết luận hàm số là chẵn.
+ Nếu f(−x)=−f(x) thì kết luận hàm số là lẻ.