Giải các bất phương trình sau :
2x + 4x2 > 8
x + x2 < 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a:=>6x^2-8x+4x-6x^2<-4
=>-4x<-4
=>x>1
b: =>6x+8x^2-8x^2-24x>5
=>-18x>5
=>x<-5/18

a)\(6x^2-8x+2x\left(2-3x\right)< -4\)
\(\Leftrightarrow6x^2-8x+4x-6x^2< -4\)
\(\Leftrightarrow-4x< -4\)
\(\Leftrightarrow-4x.\dfrac{-1}{4}>-4\cdot\dfrac{-1}{4}\)
\(\Leftrightarrow x>1\)
Vậy bất phương trình có nghiệm là \(S=\left\{xIx>1\right\}\)
b)\(2\left(3x+4x^2\right)-8x\left(x+3\right)>5\)
\(\Leftrightarrow6x+8x^2-8x^2-24x>5\)
\(\Leftrightarrow-18x>5\)
\(\Leftrightarrow-18x\cdot\dfrac{-1}{18}< 5\cdot\dfrac{-1}{18}\)
\(\Leftrightarrow x< -\dfrac{5}{18}\)
Vậy bất phương trình có nghiệm là \(S=\left\{xIx< -\dfrac{5}{18}\right\}\)

Ta có bất phương trình đã cho tương đương với
4 x 2 + 3 . 3 x + x . 3 x - 2 x 2 . 3 x - 2 x - 6 < 0
⇔ 3 + x - 2 x 2 3 x − 2(x − 2 x 2 + 3) < 0
⇔(−2 x 2 + x + 3)( 3 x − 2) < 0
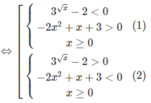
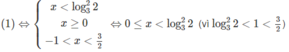
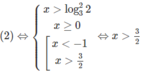
Vậy nghiệm của bất phương trình là x > 3/2 hoặc
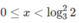

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
tự trả lời :
2x + 4x2 >8
2x(1 + 2x) >8
TH1 : 2x > 8
x > 4
TH2 : 1 + 2x >8
2x > 7
x > \(\frac{7}{2}\)
\(x+x^2< 5\)
\(\Leftrightarrow x^2+x< 5\)
\(\Leftrightarrow x(x+1)< 5\)
\(\Leftrightarrow\orbr{\begin{cases}x< 5\\x+1< 5\end{cases}}\Leftrightarrow\orbr{\begin{cases}x< 5\\x< 4\end{cases}}\)
Bạn 🕎NG Hùng Dũng🔯( Team Boss ) biết làm rồi mà sao ko làm bài cuối