CHO MÌNH HỎI TẠI SAO - x - 5 \(\ge\)0 lại suy ra được x \(\le\)- 5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
23 tháng 8 2021
Đơn giản là em đang xem một lời giải sai. Việc khẳng định $P\leq 0$ hoặc $P>0$ rồi kết luận hàm số không có GTLN là sai.
Bởi vậy những câu hỏi ở dưới là vô nghĩa.
Việc gọi $P$ là hàm số lên lớp cao hơn em sẽ được học, còn bây giờ chỉ cần gọi đơn giản là phân thức/ biểu thức.
Hàm số, có dạng $y=f(x)$ biểu diễn mối liên hệ giữa biến $x$ với biến phụ thuộc $y$. Mỗi giá trị của $x$ ta luôn xác định được một giá trị tương ứng của $y$.
AH
Akai Haruma
Giáo viên
23 tháng 8 2021
$P=AB=\frac{\sqrt{x}}{\sqrt{x}-1}=1+\frac{1}{\sqrt{x}-1}$
Để $P_{\max}$ thì $\frac{1}{\sqrt{x}-1}$ max
Điều này xảy ra khi $\sqrt{x}-1$ min và có giá trị dương
$\Leftrightarrow x>1$ và $x$ nhỏ nhất
Trong tập số thực thì em không thể tìm được số lớn hơn 1 mà nhỏ nhất được. Như kiểu $1,00000000000000000000....$ (vô hạn đến không biết khi nào thì kết thúc)
Do đó $P$ không có max
Min cũng tương tự, $P$ không có min.
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
a) Tam thức \(f(x) = {x^2} - 1\) có \(\Delta = 4 > 0\)nên f(x) có 2 nghiệm phân biệt \({x_1} = - 1;{x_2} = 1\)
Mặt khác a=1>0, do đó ta có bảng xét dấu:
Tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right] \cup \left[ {1; + \infty } \right)\)
b) Tam thức \(g(x) = {x^2} - 2x - 1\) có \(\Delta = 8 > 0\) nên g(x) có 2 nghiệm phân biệt \({x_1} = 1 - \sqrt 2 ;{x_2} = 1 + \sqrt 2 \)
Mặt khác a = 1 > 0, do đó ta có bảng xét dấu:
Tập nghiệm của bất phương trình là \(\left( {1 - \sqrt 2 ;1 + \sqrt 2 } \right)\)
c) Tam thức \(h(x) = - 3{x^2} + 12x + 1\) có\(\Delta ' = 39 > 0\)nên h(x) có 2 nghiệm phân biệt \({x_1} = \frac{{6 - \sqrt {39} }}{3};{x_2} = \frac{{6 + \sqrt {39} }}{3}\)
Mặt khác a = -3 < 0, do đó ta có bảng xét dấu:
Tập nghiệm của bất phương trình là \(\left( { - \infty ; \frac{{6 - \sqrt {39} }}{3}} \right] \cup \left[ {\frac{{6 + \sqrt {39} }}{3}; + \infty } \right)\)
d) Tam thức \(k(x) = 5{x^2} + x + 1\) có \(\Delta = - 19 < 0\), hệ số a=5>0 nên k(x) luôn dương ( cùng dấu với a) với mọi x, tức là \(5{x^2} + x + 1 > 0\) với mọi \(x \in \mathbb{R}\). Suy ra bất phương trình có vô số nghiệm
TH
17 tháng 3 2023
các cạnh tương ứng tỉ lệ với nhau, mà ta tính các góc cũng dựa vào các tỉ lệ đó, nên 2 góc của tam giác đồng dạng bằng nhau
22 tháng 4 2022
ờ thì do 2x^2 =2x.2x- 1x cho nên có thừa số chung là x nên như v
22 tháng 4 2022
có j thì bn kết bn với mình mình chỉ cho tk : ntd11223344
NT
12 tháng 3 2017
Sau giờ thứ nhất thì quãng đường còn lại là :
1 - \(\frac{2}{5}=\frac{3}{5}\)( quãng đường )
Giờ thứ hai bác Hùng đi được số phần quãng đường là :
\(\frac{3}{5}\)x \(\frac{1}{2}\)= \(\frac{3}{10}\)( quãng đường )
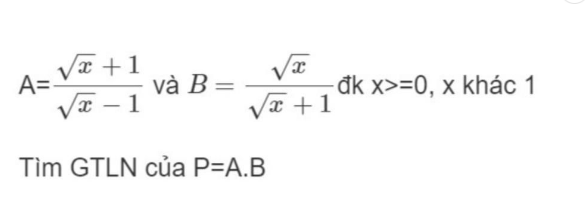
\(-x-5\ge0\Leftrightarrow-x\ge5\)(chuyển -5 qua vế phải và đổi dấu)
\(\Leftrightarrow x\le-5\)(cùng nhân 2 vế của BĐT cho -1 và BĐT đổi chiều)
Vậy hai bất phương trình \(-x-5\ge0\) và \(x\le-5\)tương đương với nhau
Ta có:\(-x-5\ge0\)
\(\Leftrightarrow-x\ge5\)
\(\Leftrightarrow\left(-1\right)\left(-x\right)\le\left(-1\right)5\)(Nhân cả hai vế cho -1)
\(\Leftrightarrow x\le-5\)
Vậy hai Bất phương trình trên tương đương với nhau