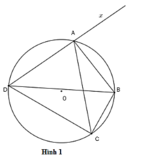
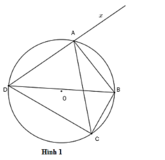
Cho tứ giác ABCD nội tiếp đường tròn (O;R) có hai đường chéo AC, BD vuông góc với nhau tại I (I khác O). Kẻ đường kính CE.
1. Chứng minh tứ giác ABDE là hình thang cân
2.Chứng minh \(\sqrt{AB^2+CD^2+BC^2+DA^2}=2\sqrt{2}R\)
3. Từ A và B kẻ đường thẳng vuông góc với CD lần lượt cắt BD tại F, cắt AC tại K. Tứ giác ABKE là hình gì?



2. Chứng minh \(\sqrt{AB^2+CD^2+BC^2+DA^2}=2\sqrt{2}R\)
Vì \(ABDE\)hình thang cân \(\Rightarrow AB=DE;AD=BE\)
Khi đó \(AB^2+CD^2+BC^2+DA^2=DE^2+CD^2+BC^2+BE^2\)
Có \(\widehat{CBE}=\widehat{CDE}\)( 2 góc nội tiếp chắn nửa đường tròn )
\(\Rightarrow\Delta BCE\)vuông tại B và \(\Delta CDE\)vuông tại D
Áp dụng định lý Py - ta - go cho 2 tam giác vuông trên ta được :
\(\hept{\begin{cases}DE^2+CD^2=CE^2=\left(2R\right)^2=4R^2\\BC^2+BE^2=EC^2=\left(2R\right)^2=4R^2\end{cases}\Rightarrow DE^2+CD^2+BC^2+BE^2=4R^2+4R^2}\)
\(\Leftrightarrow DE^2+CD^2+BC^2+BE^2=8R^2\)
\(\Rightarrow\sqrt{DE^2+CD^2+BC^2+BE^2}=\sqrt{8R^2}\)
\(\Leftrightarrow\sqrt{DE^2+CD^2+BC^2+BE^2}=2\sqrt{2}R\)
Hay \(\sqrt{AB^2+CD^2+BC^2+DA^2}=2\sqrt{2}R\)\(\left(dpcm\right)\)
Bạn tự vẽ hình nhá :
1 . Chứng minh tứ giác ABDE Là hình thang cân
Xét (O) có \(\widehat{CAE}=90^o\)( góc nột tiếp chắn nửa đường tròn )
\(\Rightarrow AE\perp AC\)
Mà \(BD\perp AC\left(gt\right)\Rightarrow AE//BD\)
Xét tứ giác \(ABDE\)có \(AE//BD\Rightarrow\)tứ giác \(ABDE\)là hình thang
Ta có : \(\widehat{CDE}=90^o\)( góc nột tiếp chắn nửa đường tròn ) \(\Rightarrow\Delta CDE\)vuông tại D
Mặt khác \(\widehat{CED}=\widehat{CBD}\)( cùng chắn cung \(\widebat{CD}\))
\(\Rightarrow90^o-\widehat{CED}=90^o-\widehat{CBD}\)
\(\Rightarrow\widehat{DCE}=\widehat{ACD}\Rightarrow\widebat{DE}=\widebat{AB}\Rightarrow sd\widebat{DE}=sd\widebat{AB}\)
Do đó \(DE=AB\Rightarrow DE+AE=AB+AE\Rightarrow AD=BE\)
\(\Rightarrow\widehat{ABD}=\widehat{EDB}\)( 2 góc nội tiếp chắn 2 cung bằng nhau )
Xét hình thang \(ABDE\)có : \(\widehat{ABD}=\widehat{EDB}\Rightarrow\)Hình thang \(ABDE\)là hình thang cân ( dpcm)