Tìm m để tổng GTLN và GTNN của y= x^4 -m^2x^3 -2x^2 -m trên đoạn [0,1] bằng -16
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KH
1
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 4 2020
Câu 2:
\(A-4=2x+3y\Rightarrow\left(A-4\right)^2=\left(2x+3y\right)^2\)
\(\left(A-4\right)^2\le\left(2^2+3^2\right)\left(x^2+y^2\right)=676\)
\(\Rightarrow-26\le A-4\le26\)
\(\Rightarrow-22\le A\le30\)
\(A_{max}=30\) khi \(\left\{{}\begin{matrix}x=4\\y=6\end{matrix}\right.\)
\(A_{min}=-22\) khi \(\left\{{}\begin{matrix}x=-4\\y=-6\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 4 2020
\(2x+3y=1\Rightarrow y=\frac{1-2x}{3}\)
Do \(x;y\ge0\Rightarrow0\le x\le\frac{1}{2}\)
\(A=x^2+3\left(\frac{1-2x}{3}\right)^2=x^2+\frac{1}{3}\left(4x^2-4x+1\right)=\frac{7}{3}x^2-\frac{4}{3}x+\frac{1}{3}\)
\(A=\frac{7}{3}\left(x-\frac{2}{7}\right)^2+\frac{1}{7}\ge\frac{1}{7}\)
\(\Rightarrow A_{min}=\frac{1}{7}\) khi \(x=\frac{2}{7};y=\frac{1}{7}\)
Mặt khác \(A=\frac{1}{3}x\left(7x-4\right)+\frac{1}{3}\)
Do \(x\le\frac{1}{2}\Rightarrow7x-4< 0\Rightarrow x\left(7x-4\right)\le0\)
\(\Rightarrow A\le\frac{1}{3}\Rightarrow A_{max}=\frac{1}{3}\) khi \(x=0;y=\frac{1}{3}\)
NH
1
KH
1
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 1 2021
\(y\le\sqrt{2\left(6-2x+3+2x\right)}=3\sqrt{2}\)
\(y_{max}=3\sqrt{2}\) khi \(x=\dfrac{3}{4}\)
\(y\ge\sqrt{6-2x+3+2x}=3\)
\(y_{min}=3\) khi \(\left[{}\begin{matrix}x=3\\x=-\dfrac{3}{2}\end{matrix}\right.\)
DT
19 tháng 7 2016
\(1.A=x^2+3x-1=-\left(x^2-2.x.\frac{3}{2}+\frac{3}{2}^2-\frac{5}{4}\right)\)
\(A=-\left(x-\frac{3}{2}\right)^2+\frac{5}{4}\)
Vì \(\left(x-\frac{3}{2}\right)^2\ge0,x\in R\)
do đó \(-\left(x-\frac{3}{2}\right)^2\le0,x\in R\)
nên \(-\left(x-\frac{3}{2}\right)^2+\frac{5}{4}\le\frac{5}{4},x\in R\)
Vậy \(Max_A=\frac{5}{4},x=\frac{3}{2}\)
CM
5 tháng 6 2018
Đáp án B.
Phương pháp:
Sử dụng cách vẽ đồ thị hàm số y = f x
Cách giải:
Xét hàm số y = x 2 + 2 x + m − 4 = f x có:
y ' = 2 x + 2
y ' = 0 ⇔ x = − 1
Bảng biến thiên:
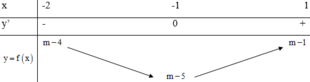
+) m ≥ 5 :
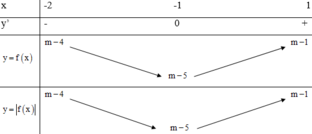
M a x − 2 ; 1 x 2 + 2 x + m − 4 = f 1 = m − 1 = 4 ⇒ m = 5
(Thỏa mãn)
+) 4 ≤ m < 5 :
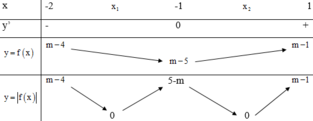
M a x − 2 ; 1 x 2 + 2 x + m − 4 = M a x m − 1 ; 5 − m = 4
Mà
m − 1 > 5 − m , ∀ m ∈ 4 ; 5 ⇒ m − 1 = 4 ⇒ m = 5
(loại)
+) 1 ≤ m < 4 :
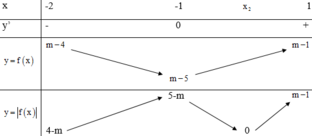
M a x − 2 ; 1 x 2 + 2 x + m − 4 = M a x 5 − m ; m − 1 = 4.
m ∈ − 1 ; 3 ⇒ max y = 5 − m = 4 ⇔ m = 1 t m
m ∈ − 1 ; 3 ⇒ max y = m − 1 = 4 ⇔ m = 5 k t m
+) m < 1 :
M a x − 2 ; 1 x 2 + 2 x + m − 4 = 5 − m = 4 ⇒ m = 1
(Không thỏa mãn)
Vậy m ∈ 4 ; 1 , có hai giá trị của m thỏa mãn.
TT
0
NV
1
17 tháng 1 2018
Ta có: \(M=\frac{x^2+2x+3}{x^2+2}=\frac{2.\left(x^2+2\right)-\left(x^2-2x+1\right)}{x^2+2}\)
\(=\frac{2.\left(x^2+2\right)}{x^2+2}-\frac{x^2-2x+1}{x^2+2}=2-\frac{\left(x-1\right)^2}{x^2+2}\le2\)
Dấu "=" xảy ra khi \(x-1=0\Rightarrow x=1\)
Vậy Mmax = 2 khi x = 1
\(y'=4x^3-3m^2x^2-4x\)
\(y'=0\Rightarrow x\left(4x^2-3m^2x-4\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\4x^2-3m^2x-4=0\end{matrix}\right.\)
Xét pt \(f\left(x\right)=4x^2-3m^2x-4=0\)
Do \(ac=-16< 0\Rightarrow\) pt luôn có 2 nghiệm trái dấu
Gọi \(x_2\) là nghiệm dương \(\Rightarrow x=x_2\) là điểm cực tiểu của hàm số
Do \(f\left(1\right)=-3m^2\le0\) \(\forall m\Rightarrow x_2\ge1\) \(\forall m\)
\(\Rightarrow y\) nghịch biến trên \(\left[0;1\right]\Rightarrow\max\limits_{\left[0;1\right]}y=y\left(0\right)=-m\)
\(\min\limits_{\left[0;1\right]}y=y\left(1\right)=-m^2-m-1\)
\(\Rightarrow-m^2-2m-1=-16\Leftrightarrow m^2+2m-15=0\Rightarrow\left[{}\begin{matrix}m=3\\m=-5\end{matrix}\right.\)