Giải phương trình
1: 4sin2x + 8cos2x - 9 = 0
2: 1-5sinx + 2cos2x = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
(k ∈ Z)
24 tháng 7 2017
a. cos2x = 1-sin2x
b. cos2x = 2cos2x - 1
c. 2cosx.cos2x = 1 + cos2x + cos3x
=> 2cosx.cos2x = 2cos2x + 4cos3x - 3cosx
=> cosx(2.(2cos2x - 1) - 2cosx - 4cos2x +3) = 0
=> cosx( -2cosx + 1) = 0
=> cosx=0 hoặc cosx = -1/2
CM
11 tháng 12 2019
8cos2x + 2sinx – 7 = 0 (1)
⇔ 8(1 – sin2x) + 2sinx – 7 = 0
⇔ 8sin2x - 2sinx – 1 = 0 (Phương trình bậc hai với ẩn sin x)
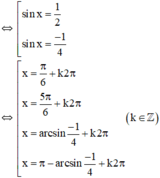
Vậy phương trình có tập nghiệm
{
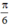+ k2π; 
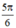+ k2π; arcsin
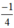+ k2π; π - arcsin
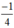+ k2π (k ∈ Z).
CM
11 tháng 3 2019
2cos2x – 3cosx + 1 = 0 (Phương trình bậc hai với ẩn cos x).
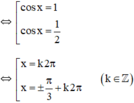
Vậy phương trình có tập nghiệm
CM
5 tháng 8 2018
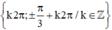
Hướng dẫn giải:
Chọn A.
+ Trường hợp 1.
: là nghiệm của phương trình
+ Trường hợp 2.
: Chia 2 vế phương trình cho cos2x ta được
CM
9 tháng 3 2018
2cos2x – 3cosx + 1 = 0 (1)
đặt t = cosx, điều kiện –1 ≤ t ≤ 1
(1) trở thành 2t2 – 3t + 1 = 0
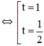(thỏa mãn điều kiện).
+ t = 1 ⇒ cos x = 1 ⇔ x = k.2π (k ∈ Z)
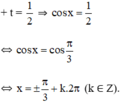
Vậy phương trình có tập nghiệm
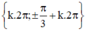(k ∈ Z).
1. 4sin2x + 8cos2x-9=0
⇔ 4(sin2x+cos2x) + 4cos2x = 9
⇔ cos2x= \(\frac{9}{4}\)
⇔ cosx= \(\left[{}\begin{matrix}cosx=\frac{3}{2}\left(KTM\right)\\cosx=\frac{-3}{2}\left(KTM\right)\end{matrix}\right.\)
Vậy pt vô nghiệm
2.
1-5sinx + 2cos2x=0
⇔1- 5sinx + 2(1-sin2x)=0
⇔ 2sin2x + 5sinx -3 =0
⇔\(\left[{}\begin{matrix}sinx=0,5\\sinx=-3\left(ktm\right)\end{matrix}\right.\)
Có sinx=0,5
⇔x=\(\left[{}\begin{matrix}x=\frac{\pi}{6}+2k\pi\\\frac{5\pi}{6}+2k\pi\end{matrix}\right.\left(k\in z\right)\)
Bạn sửa lại giúp mình câu 2 chỗ x đó là dấu ngoặc nhọn nhé, không phải dấu ngoặc vuông. Mình bị nhầm.