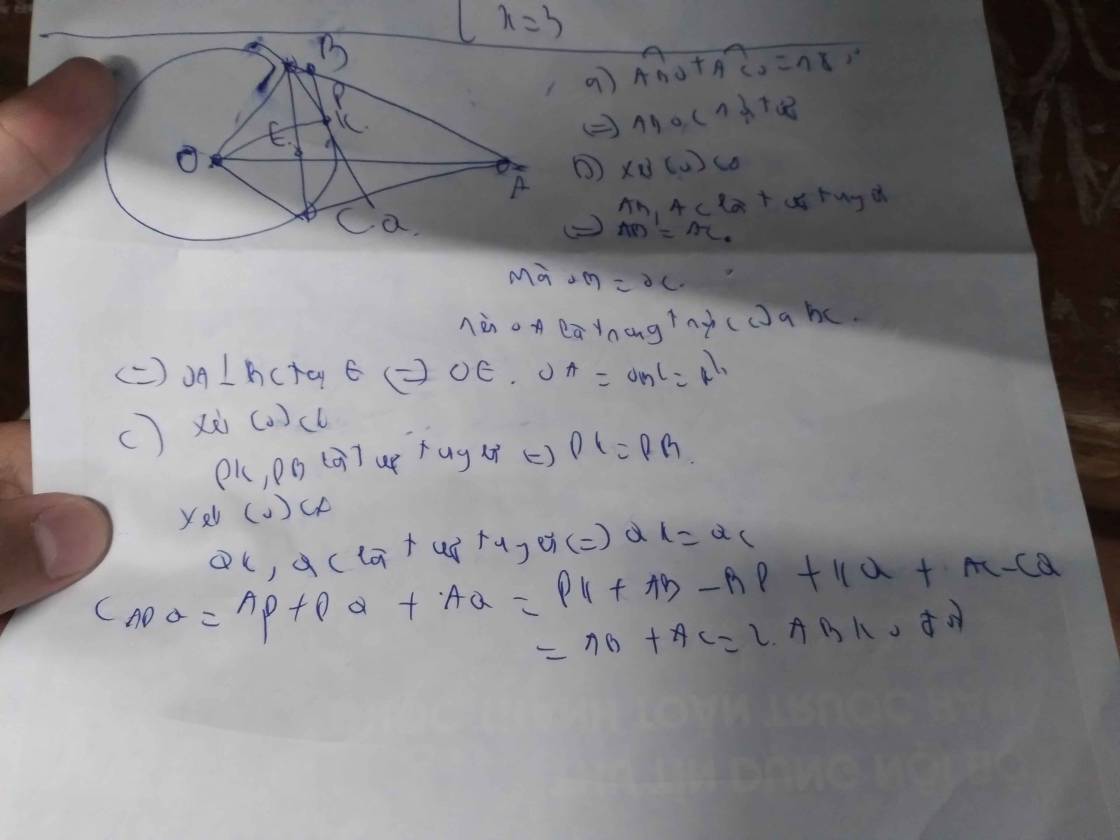
Từ một điểm A nằm ngoài đường tròn tâm O bán kính R, kẻ các tiếp tuyến AB, AC với đường tròn (B ,C là các tiếp điểm). Trên cung nhỏ BC lấy một điểm M bất kỳ khác B và C. Gọi I, K, P lần lượt là hình chiếu vuông góc của điểm M trên các đoạn thẳng AB, AC, BC. 1. Chứng minh AIMK là tứ giác nội tiếp. 2. Chứng Minh \(\widehat{MPK}\)= \(\widehat{MBC}\) 3. xác định vị trí M trên cung nhỏ BC để tích MI.MK.MP đạt giá trị lớn nhất.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc BEI+góc BDI=180 độ
=>BEID nội tiếp
góc CEI+góc CFI=180 độ
=>CEIF nội tiếp
b: góc IED=góc IBD=1/2*sđ cung BI
góc IFE=góc ICE=1/2*sđ cung BI
=>góc IED=góc IFE
góc IDE=góc IBE=1/2*sđ cung IC
góc IEF=góc ICF=1/2*sđ cung IC
=>góc IDE=góc IEF
=>ΔIDE đồng dạng với ΔIEF

+) Bước 1: Chứng minh \(\Delta\) FPO vuông tại P
Ta có: \(\widehat{O_1}=\widehat{FOP}=\widehat{FOE}=\widehat{FOM}+\widehat{MOE}=\frac{1}{2}\widehat{COM}+\frac{1}{2}\widehat{MOB}=\frac{1}{2}\widehat{BOC}\)
=> \(\widehat{FOP}=\frac{1}{2}\widehat{BOC}\)
mà \(\widehat{FCP}=\widehat{FCB}=\frac{1}{2}\widehat{BOC}\) ( góc nội tiếp = 1/2 góc ở tâm khi chắn cùng một cung)
=> \(\widehat{FOP}=\widehat{FCP}\)
=> Tứ giác CFPO nội tiếp => \(\widehat{FPO}+\widehat{FCO}=180^o\Rightarrow\widehat{FPO}=180^o-90^o=90^o\)
=> \(\Delta\) FPO vuông tại P
+) Bước 2: Chứng minh \(\Delta\) EQO vuông tại Q. ( Chứng minh tương tự)
+) Bước 3: Chứng minh tỉ số: \(\frac{PQ}{EF}=\frac{OQ}{OE}\)
Xét \(\Delta\) FPO vuông tại P và \(\Delta\) EQO vuông tại Q có: \(\widehat{O_1}\) chung
=> \(\Delta\) FPO ~ \(\Delta\) EQO
=> \(\frac{OQ}{OE}=\frac{OP}{OF}\)
Xét \(\Delta\) OQP và \(\Delta\) OEF có: \(\frac{OQ}{OE}=\frac{OP}{OF}\)( chứng minh trên ) và \(\widehat{O_1}\) chung
=> \(\Delta\) OQP ~ \(\Delta\) OEF
=> \(\frac{PQ}{EF}=\frac{OQ}{OE}\)(1)
+) Bước 4: Chứng minh Tỉ số \(\frac{PQ}{EF}\)không đổi khi M di chuyển trên cung nhỏ BC
Xét \(\Delta\)EQO vuông tại Q => \(\cos\widehat{O_1}=\frac{OQ}{OE}\)
Mặt khác : \(\widehat{O_1}=\frac{1}{2}\widehat{BOC}\) ( xem chứng minh ở Bước 1)
=> \(\cos\frac{1}{2}.\widehat{BOC}=\frac{OQ}{OE}\) (2)
Từ (1) ; (2) => \(\frac{PQ}{EF}=\cos\frac{1}{2}.\widehat{BOC}\)không đổi khi M di chuyển. ::))

Ta có: \(OB=OC=R\) ; \(AB=AC\) (t/c hai tiếp tuyến cắt nhau)
\(\Rightarrow OA\) là trung trực của BC
\(\Rightarrow OA\) là phân giác góc \(\widehat{BAC}\) (1)
Mặt khác I thuộc OA \(\Rightarrow IB=IC\Rightarrow\Delta IBC\) cân tại I
\(\Rightarrow\widehat{CBI}=\widehat{BCI}\)
Mà \(\widehat{BCI}=\widehat{ABI}\) (góc nội tiếp và góc tiếp tuyến cùng chắn cung BI)
\(\Rightarrow\widehat{CBI}=\widehat{ABI}\Rightarrow BI\) là phân giác \(\widehat{ABC}\) (2)
(1);(2) \(\Rightarrow I\) là tâm đường tròn nội tiếp tam giác ABC
https://h.vn/hoi-dap/tim-kiem?q=t%E1%BB%AB+1+%C4%91i%E1%BB%83m+A+n%E1%BA%B1m+ngo%C3%A0i+(O;R)+ta+v%E1%BA%BD+hai+ti%E1%BA%BFp+tuy%E1%BA%BFn+AB,AC+v%E1%BB%9Bi+%C4%91%C6%B0%E1%BB%9Dng+tr%C3%B2n+(B,C+l%C3%A0+ti%E1%BA%BFp+%C4%91i%E1%BB%83m+).tr%C3%AAn+cung+nh%E1%BB%8F+BC+l%E1%BA%A5y+m%E1%BB%99t+%C4%91i%E1%BB%83m+M,v%E1%BA%BD+MI+vu%C3%B4ng+g%C3%B3c+v%E1%BB%9Bi+AB,MK+vu%C3%B4ng+g%C3%B3c+v%E1%BB%9Bi+AC(I+thu%E1%BB%99c+AB,K+thu%E1%BB%99c+AC)+a,ch%C3%BAng+minh+AIMK+l%C3%A0+t%E1%BB%A9+gi%C3%A1c+n%E1%BB%99i+ti%E1%BA%BFp+%C4%91%C6%B0%E1%BB%9Dng+tr%C3%B2n+b,v%E1%BA%BD+MP+vu%C3%B4ng+g%C3%B3c+v%E1%BB%9Bi+BC(P+thu%E1%BB%99c+BC).ch%E1%BB%A9ng+minh+g%C3%B3c+MPK=g%C3%B3c+MBC+c,x%C3%A1c+%C4%91%E1%BB%8Bnh+v%E1%BB%8B+tr%C3%AD+%C4%91i%E1%BB%83m+M+tr%C3%AAn+cung+nh%E1%BB%8F+BC+%C4%91%E1%BB%83+t%C3%ADch+MI.MK.MP+%C4%91%E1%BA%A1t+GTLN&id=249466
Bạn xem ở link này nhé(Mình sẽ gửi vào tin nhắn)
Học tốt@!!!!!!!!!