cho hai số thực x,y thỏa mãn x+y=5 và x4 +y4 +x2 +y2=110. Tính giá trị của biểu thức P=x5 +y5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
A
3 tháng 8 2023
\(\text{a) x^2 + y^2 = (x+y)^2 - 2xy = a^2 - 2b}\)
\(\text{b) x^3 + y^3 = (x+y)^3 - 3xy(x+y) = a^3 - 3ab}\)
\(\text{c) x^4 + y^4 = (x^2+y^2)^2 - 2x^2y^2 = (a^2-2b)^2 - 2b^2 = a^4 - 4a^2b + 2b^2}\)
\(\text{d) x^5 + y^5 = (x^3+y^3)(x^2+y^2) - x^2y^2(x+y) = a^5 - 5a^3b + 5ab^2}\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 9 2021
\(x^5+y^5=\left(x^2+y^2\right)\left(x^3+y^3\right)-x^2y^3-x^3y^2\)
\(=\left(x^2+y^2\right)\left(x^3+y^3\right)-\left(xy\right)^2\left(x+y\right)\)
\(=10.26-\left(-3\right)^2.2=...\)
11 tháng 9 2021
(x+y)5=32
⇔ x5+5x4y+10x3y2+10x2y3+5xy4+y5 = 32
⇔ x5+y5 = 32-5xy(x3+y3)-10x2y2(x+y)
= 32-5.(-3).26-10.(-3)2.2
= 242
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2020
\(x^2+y^2=1+xy\Rightarrow x^2+y^2-xy=1\)
Ta có: \(1+xy=x^2+y^2\ge2xy\Rightarrow xy\le1\)
\(1+xy=x^2+y^2\ge-2xy\Rightarrow xy\ge-\dfrac{1}{3}\)
\(P=\left(x^2+y^2\right)^2-x^2y^2-2x^2y^2=\left(x^2+y^2-xy\right)\left(x^2+y^2+xy\right)-2x^2y^2\)
\(=x^2+y^2+xy-2x^2y^2=-2x^2y^2+2xy+1\)
Đặt \(a=xy\Rightarrow P=f\left(a\right)=-2a^2+2a+1\)
Xét hàm \(f\left(a\right)=-2a^2+2a+1\) trên \(\left[-\dfrac{1}{3};1\right]\)
\(-\dfrac{b}{2a}=\dfrac{1}{2}\in\left[-\dfrac{1}{3};1\right]\)
\(f\left(-\dfrac{1}{3}\right)=\dfrac{1}{9}\) ; \(f\left(\dfrac{1}{2}\right)=\dfrac{3}{2}\) ; \(f\left(1\right)=1\)
\(\Rightarrow M=\dfrac{3}{2}\) ; \(m=\dfrac{1}{9}\) \(\Rightarrow Mm=\dfrac{1}{6}\)
CM
17 tháng 10 2017
Ta có ( x + y ) 2 = x 2 + y 2 + 2 x y = 4 − 2 3 = ( 3 − 1 ) 2 ⇒ x + y = 3 − 1.
Suy ra P = x + y = 3 − 1 k h i x + y ≥ 0 1 − 3 k h i x + y < 0 .
TD
2
23 tháng 11 2023
a) Để tính giá trị của biểu thức x^4 + y^4, ta có thể sử dụng công thức Newton về tổng lũy thừa của một đa thức. Theo công thức Newton, ta có: x^4 + y^4 = (x^2 + y^2)^2 - 2x^2y^2 Từ đó, ta có thể tính giá trị của biểu thức x^4 + y^4 theo a và b: x^4 + y^4 = (a^2 - 2b)^2 - 2(a - 2b)b b) Tương tự, để tính giá trị của biểu thức x^5 + y^5, ta có thể sử dụng công thức Newton về tổng lũy thừa của một đa thức. Theo công thức Newton, ta có: x^5 + y^5 = (x + y)(x^4 - x^3y + x^2y^2 - xy^3 + y^4) Từ đó, ta có thể tính giá trị của biểu thức x^5 + y^5 theo a và b: x^5 + y^5 = (a)(a^4 - a^3b + a^2b^2 - ab^3 + b^4)
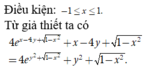
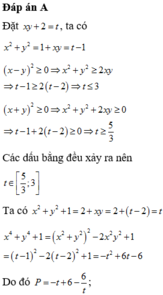
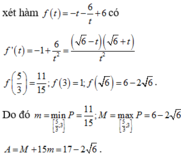
\(x^2+y^2=\left(x+y\right)^2-2xy=25-2xy\)
\(x^4+y^4=\left(x^2+y^2\right)^2-2x^2y^2=\left(25-2xy\right)^2-2x^2y^2\)
\(\Rightarrow x^4+y^4=2x^2y^2-100xy+625\)
Thay vào ta được:
\(2x^2y^2-100xy+625+25-2xy=110\)
\(\Leftrightarrow2x^2y^2-102xy+540=0\Rightarrow\left[{}\begin{matrix}xy=45>\frac{\left(x+y\right)^2}{4}\left(l\right)\\xy=5\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x+y=5\\xy=6\end{matrix}\right.\) \(\Rightarrow\left(x;y\right)=\left(2;3\right);\left(3;2\right)\)
\(\Rightarrow P=2^5+3^5=275\)