So sánh: \(2\sqrt{3}\) và \(3\sqrt{2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\left(\sqrt{2}+\sqrt{3}\right)^2=5+2\sqrt{6}>2^2=4\left(5>4\right)\\ \Leftrightarrow\sqrt{2}+\sqrt{3}>2\)
\(\left(\sqrt{8}+\sqrt{5}\right)^2=13+2\sqrt{40};\left(\sqrt{7}-\sqrt{6}\right)^2=13-2\sqrt{42}\\ 2\sqrt{40}>0>-2\sqrt{42}\\ \Leftrightarrow13+2\sqrt{40}>13-2\sqrt{42}\\ \Leftrightarrow\left(\sqrt{8}+\sqrt{5}\right)^2>\left(\sqrt{7}-\sqrt{6}\right)^2\\ \Leftrightarrow\sqrt{8}+\sqrt{5}>\sqrt{7}-\sqrt{6}\)

Đặt:
\(A=\sqrt{3+\sqrt{5}}+\sqrt{3-\sqrt{5}}\)
\(A=\dfrac{1}{\sqrt{2}}\left(\sqrt{6+2\sqrt{5}}+\sqrt{6-2\sqrt{5}}\right)\)
\(A=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(1+\sqrt{5}\right)^2}+\sqrt{\left(\sqrt{5}-1\right)^2}\right)\)
\(A=\dfrac{1}{\sqrt{2}}\left(\left|1+\sqrt{5}\right|+\left|\sqrt{5}-1\right|\right)\)
\(A=\dfrac{1}{\sqrt{2}}\left(1+\sqrt{5}+\sqrt{5}-1\right)\)
\(A=\dfrac{2\sqrt{5}}{\sqrt{2}}=\sqrt{10}\)
Ta có: \(A^2=\left(\sqrt{10}\right)^2=10\)
\(B=\left(2+\sqrt{5}\right)^2=9+4\sqrt{5}\)
Mà: \(4\sqrt{5}>1\)
Nên: \(A^2< B^2\)
\(\Rightarrow A< B\)
Đặt \(A=\sqrt{3+\sqrt{5}}+\sqrt{3-\sqrt{5}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{6+2\sqrt{5}}+\sqrt{6-2\sqrt{5}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{5}+1+\sqrt{5}-1\right)=\dfrac{2\sqrt{5}}{\sqrt{2}}=\sqrt{10}\)
=>A^2=(căn 10)^2=10=9+1
Đặt B=2+căn 5
=>B^2=(2+căn 5)^2=9+4căn 5
1<4căn 5
=>9+1<9+4căn 5
=>A^2<B^2
=>A<B

Bài này cũng không dài mìn nghĩ bạn nên làm tất cho đầy đủ chứ làm 1 phần như nayd quá ngắn

\(2\sqrt{3}=\sqrt{2^2.3}=\sqrt{12}\)
\(3\sqrt{2}=\sqrt{3^2.2}=\sqrt{18}\)
--> \(2\sqrt{3}< 3\sqrt{2}\)
.-.còn cách giải nào dễ hiểu hơn nữa không đọc xong mù luôn cả chữ

a: \(1< \sqrt{2}\)
nên \(2< \sqrt{2}+1\)
b: \(2\sqrt{31}=\sqrt{124}\)
\(10=\sqrt{100}\)
mà 124>100
nên \(2\sqrt{31}>10\)
c: \(-3\sqrt{11}=-\sqrt{99}\)
\(-\sqrt{12}=-\sqrt{12}\)
mà 99>12
nên \(-3\sqrt{11}< -\sqrt{12}\)

a)
Có: \(2>1>0\)
\(\Rightarrow\sqrt{2}>1\Rightarrow1+\sqrt{2}>1+1\\ \Leftrightarrow1+\sqrt{2}>2\)
b) Có: \(0< \sqrt{3}< 3\)
\(\Rightarrow3+1>\sqrt{3}+1\\ \Rightarrow4>\sqrt{3}+1\)
c) Có: \(0< \sqrt{11}< \sqrt{25}\left(0< 11< 25\right)\)
\(\Rightarrow\sqrt{11}< 5\\ \Rightarrow-2\sqrt{11}>-2.5=-10\left(-2< 0\right)\)
d) Có: \(0< \sqrt{11}< \sqrt{16}=4\left(do.0< 11< 16\right)\)
\(\Rightarrow3\sqrt{11}< 3.4\\ \Leftrightarrow3\sqrt{11}< 12\)
a: 2=1+1<1+căn 2
b: 4=1+3>1+căn 3
c: -2căn 11=-căn 44
-10=-căn 100
mà 44<100
nên -2 căn 11>-10
d: 12=3*4=3*căn 16>3*căn 11

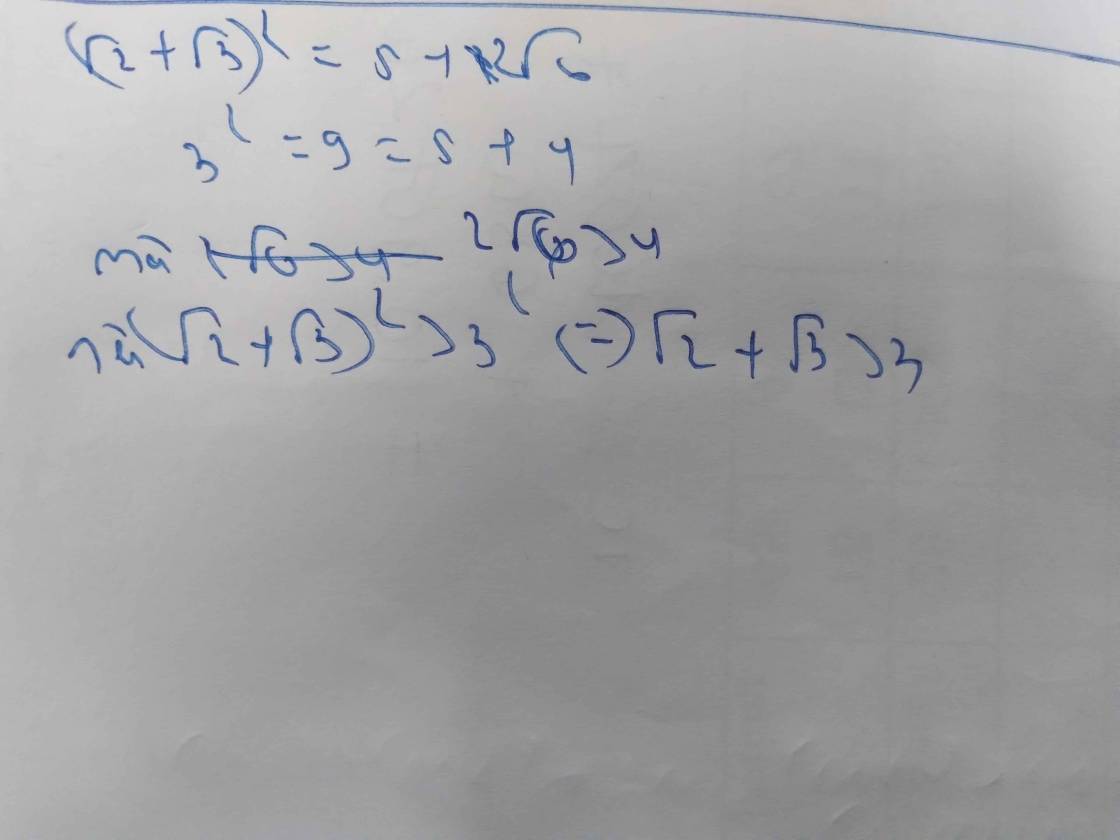
#)Giải :
Bình phương hai vế, ta được :
\(\left(3\sqrt{2}\right)^2\)và \(\left(2\sqrt{3}\right)^2\)
\(\Leftrightarrow18\)và \(12\)
Vì 18 > 12 => 3√2 > 2√3
Ta có: \(2\sqrt{3}=\sqrt{4}.\sqrt{3}=\sqrt{12}\)
\(3\sqrt{2}=\sqrt{9}.\sqrt{2}=\sqrt{18}\)
Vì 12 < 18 nên \(\sqrt{12}< \sqrt{18}\)
Vậy \(2\sqrt{3}< 3\sqrt{2}\)