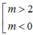cho hệ phương trình : 3x-y= 2m-1
x+2y=3m+2
tìm điểm có tọa độ (x,y) nằm trong góc phần tư thứ hai của mặt phẳng toạn độ và thỏ mãn 3x2+y2=2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HT
4 tháng 6 2019
\(\left\{{}\begin{matrix}3-y=2m-1\\x+2y=3m+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m\\y=m+1\end{matrix}\right.\)(cái này bạn dùng phg pháp thế rùi giải ra, mình lười trình bày)
Có điểm có toạ độ (x;y) nằm trong góc phần tư thứ hai
\(\Rightarrow\left\{{}\begin{matrix}x< 0\\y>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\m+1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< 0\\m>-1\end{matrix}\right.\Leftrightarrow-1< m< 0\)
Có 3x2+y2=2
\(\Leftrightarrow3m^2+\left(m+1\right)^2=2\)
\(\Leftrightarrow3m^2+m^2+2m+1=2\)
\(\Leftrightarrow4m^2+2m-1=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=\frac{-1+\sqrt{5}}{4}=x\left(loai\right)\\m=\frac{-1-\sqrt{5}}{4}=x\left(tman\right)\end{matrix}\right.\)
\(\Rightarrow y=m+1=\frac{-1-\sqrt{5}}{4}+1=\frac{3-\sqrt{5}}{4}\left(tman\right)\)
Vậy điểm cần tìm có toạ độ(x;y)=(\(\frac{-1-\sqrt{5}}{4};\frac{3-\sqrt{5}}{4}\))
CM
23 tháng 2 2019
a, Biến đổi hệ phương trình ban đầu ta được hệ x - y = 0 3 x + 3 y = 12
Từ đó tìm được x = 2, y = 2
b, Phương trình hoành độ giao điểm của d và (p):
x 2 - 2 x - m 2 + 2 m = 0 (1)
d cắt (P) tại hai điểm phân biệt nằm về hai phía của trục tung Oy <=> (1) có hai nghiệm trái dấu. Từ đó tìm được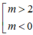 
Kết luận 