cho tam giác abc có \(\widehat{B}\) và \(\widehat{C}\) là các góc nhọn.Kẻ \(AH\perp BC\).CMR h nằm giữa b và c
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
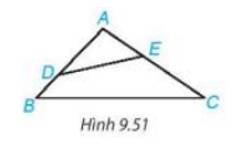
Ta có \(\widehat {BAC}\) là góc tù nên \(\widehat {ADE},\widehat {AED}\) là các góc nhọn
\( \Rightarrow \widehat {DEC}\) là góc tù
\( \Rightarrow DE < DC\) (quan hệ giữa góc và cạnh đối diện trong tam giác DEC). (1)
Xét tam giác ADC có:
\(\widehat {DAC}\) là góc tù nên \(\widehat {ADC},\widehat {ACD}\) là các góc nhọn
\( \Rightarrow \widehat {BDC}\) là góc tù.
\( \Rightarrow DC < BC\) (quan hệ giữa góc và cạnh đối diện trong tam giác BDC) (2)
Từ (1) và (2) suy ra: BC > DE
Dễ thấy H;B;C là 3 điểm phân biệt vì nếu H trùng với B hoặc C thì \(\widehat{B}=90^0\) hoặc \(\widehat{C}=90^0\)(Trái GT)
Trong 3 điểm phân biệt thì có 1 điểm nằm giữa 2 điểm kia.Giả sử C nằm giữa B và H thì
\(\widehat{ACH}< 90^0\Rightarrow\widehat{BCA}>90^0\left(false\right)\)
Giả sử B nằm giữa C và H thì \(\widehat{AHB}< 90^0\Rightarrow\widehat{CBA}>90^0\left(false\right)\)
Vậy H nằm giữa B và C.
Giả sử H nằm giữa B và C
Suy ra: góc B và góc C phải là góc tù
Trái với gt
Vậy .......