Cho f’(x) =f’(x-1) . Biết f(0)=1 ,f(1)=2019. Tính nguyên hàm tích phân từ [0,1] của f(x)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 11 2018
Chọn C.
Đặt u = G ( x ) d v = f ( x ) d x ⇒ d u = G ( x ) ' d x = g ( x ) d x v = ∫ f ( x ) d x = F ( x )
Suy ra: I = G ( x ) F ( x ) 2 0 - ∫ 0 2 F ( x ) g ( x ) d x
= G(2)F(2) – G(0)F(0) – 3 = 1 – 0 – 3 = -2.
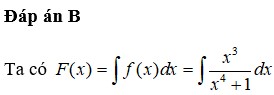
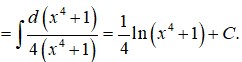
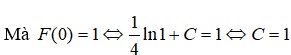
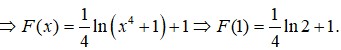
Lời giải:
\(f'(x)=f'(x-1); dx=d(x-1)\)
\(\Rightarrow f'(x)dx=f'(x-1)d(x-1)\)
\(\Rightarrow \int f'(x)dx=\int f'(x-1)d(x-1)\)
\(\Rightarrow f(x)=f(x-1)+c\)
Thay $x=1$ ta có \(f(1)=f(0)+c\Leftrightarrow 2019=1+c\Rightarrow c=2018\)
Khi đó: $f(x)=f(x-1)+2018$
\(f(0)=1=1+2018.0\)
\(f(1)=1+2018.1\)
\(f(2)=f(1)+2018=1+2018.1+2018=1+2018.2\)
.........
\(\Rightarrow f(x)=1+2018.x\)
Do đó: \(\int ^{1}_{0}f(x)dx=\int ^{1}_{0}(2018x+1)dx=\left.\begin{matrix} 1\\ 0\end{matrix}\right|(1009x^2+x)=1010\)