có bao nhiêu giá trị nguyên của m thuộc [0;2018] để bất phương trình m +\(e^{\frac{\pi}{2}}\ge\sqrt[4]{e^{2x}+1}\) có nghiệm với mọi xϵR?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 10 2019
Đáp án C
Ta có 6 x + 3 + m 2 x + m = 0 1 có nghiệm x ∈ 0 ; 1
1 ⇔ − m 2 x + 1 = 6 x + 3.2 x ⇔ − m = 6 x + 3.2 x 2 x + 1 ⇔ − m = 3 x + 3 2 − x + 1 = g x
g ' x = 3 x ln 3 1 + 2 − x + 2 − x ln 2 3 x + 3 1 + 2 − x 2 > 0 ⇒ g x đồng biến trên 0 ; 1 , g 0 = 2 , g 1 = 4
QV
Có bao nhiêu giá trị nguyên của m để pt sin2 x - sinx - 3 -m = 0 có nghiệm duy nhất thuộc [-π/2;π/2]
0
CM
9 tháng 9 2017
Nếu m = 0 thì phương trình trở thành 1 = 0 : vô nghiệm.
Khi m ≠ 0 , phương trình đã cho có nghiệm khi và chỉ khi
∆ = m 2 - 4 m ≥ 0 ⇔ m ≤ 0 m ≥ 4
Kết hợp điều kiện m ≠ 0 , ta được m < 0 m ≥ 4
Mà m ∈ Z và m ∈ [−10; 10] ⇒ m ∈ {−10; −9; −8;...; −1} ∪ {4; 5; 6;...; 10}.
Vậy có tất cả 17 giá trị nguyên m thỏa mãn bài toán.
Đáp án cần chọn là: A
CM
11 tháng 3 2019
+) Phương trình ban đầu có nghiệm khi và chỉ khi phương trình bậc hai ẩn t có nghiệm dương.
Cách giải:
6 tháng 2 2021
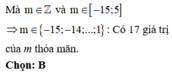
- Đặt \(a=x^2\left(a\ge0\right)\)
PTTT \(a^2-2a-2m+3=0\)
Có : \(\Delta^,=\left(-1\right)^2-\left(-2m+3\right)=1+2m-3=2m-2\)
- Theo viet : \(\left\{{}\begin{matrix}a_1+a_2=2\\a_1a_2=3-2m\end{matrix}\right.\)
- Để phương trình đề có nghiệm :
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta^,\ge0\\a_1+a_2>0\\a_1a_2\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2m-2\ge0\\3-2m\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ge1\\m\le\dfrac{3}{2}\end{matrix}\right.\)
\(\Rightarrow1\le m\le\dfrac{3}{2}\) ( * )
- Lại có : \(x^4-2x^2=3-2m\)
- Đặt \(f\left(x\right)=x^4-2x^2\)
- Ta có đồ thị của hàm số :
- Theo đồ thị hàm số để phương trình có nghiệm thuộc ( -2; 2 )
\(\Leftrightarrow-1\le3-2m\le8\)
\(\Leftrightarrow-\dfrac{5}{2}\le m\le2\) ( ** )
- Kết hợp điều kiện ( * ) và ( ** ) ta được : \(m\in\left[1;\dfrac{3}{2}\right]\)
Vậy có 1 giá trị m thỏa mãn điều kiện đề bài ( m = 1 ) .
CM
1 tháng 8 2018
Chọn B
Phương pháp:
Từ ycbt suy ra ta phải tìm m để hàm số có hai điểm cực trị dương hay phương trình y' = 0 có hai nghiệm dương phân biệt.
Ta sử dụng phương trình 
có hai nghiệm dương phân biệt
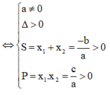
Cách giải:
Ta có 
Từ ycbt suy ra ta phải tìm m để hàm số có hai điểm cực trị dương hay phương trình y' = 0 có hai nghiệm dương phân biệt.
Khi đó
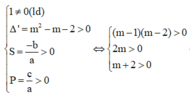
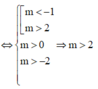
Mà 
nên có 2018 – 3 + 1 = 2016 giá trị m thỏa mãn.
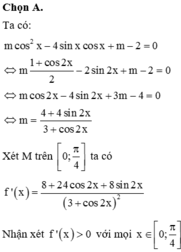
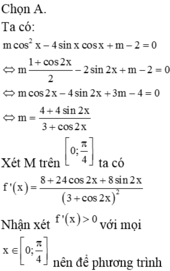
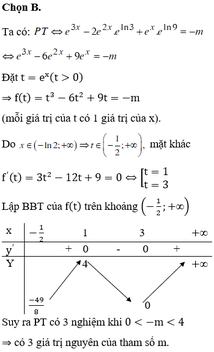
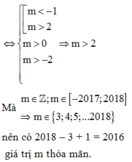
1. cô lập m: m>= -\(e^{\frac{\pi}{2}}\)+\(\sqrt[4]{e^{2x+1}}\)
2 bất phương trình có nghiệm vs mọi x=> m> max của vế phải
3 tìm max vế phải