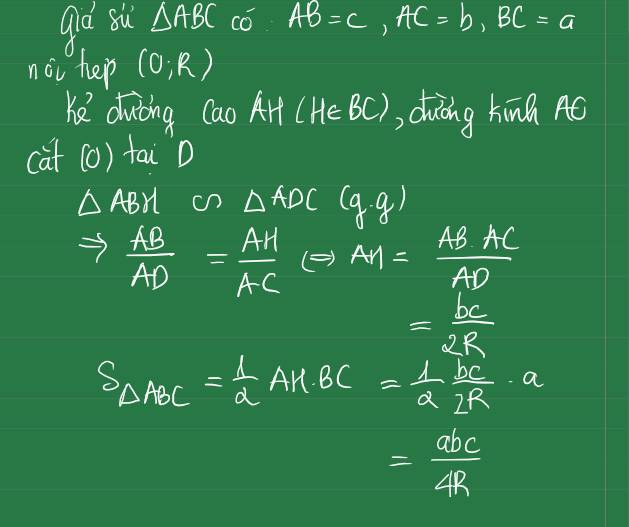tam giác ABC có độ dài các cạnh là số nguyên. tam giác ABC nội tiếp (O) có R=3,125. Tính các cạnh tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn vẽ hình nhé
Xét tam giác AOB
=> \(AO+OB>AB\)(bất đẳng thức tam giác )
=> \(AB< 6.25\) => \(a,b,c< 6.25\)
Tương tự \(AC< 6.25\),\(BC< 6.25\)
Sử dụng công thức herong và công thức tính S tam giác ta có
\(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\)(p là nửa chu vi tam giác )
\(S=\frac{abc}{4R}\)
=> \(\frac{abc}{R}=\sqrt{\left(a+b+c\right)\left(a+b-c\right)\left(a+c-b\right)\left(b+c-a\right)}\)
Mà a,b,c là các số tự nhiên , \(\frac{abc}{4R}=\frac{abc}{12.5}\)là số hữu tỉ
=> \(\sqrt{\left(a+b+c\right)\left(a+b-c\right)\left(b+c-a\right)\left(a+c-b\right)}\)là số tự nhiên
=> \(\frac{abc}{R}\)là số tự nhiên
=> \(\frac{8abc}{25}\)là số tự nhiên
Mà \(a,b,c< 6.25\)
=> 2 trong 3 số sẽ chia hết cho 5 => 2 trong 3 số sẽ bằng 5
Vì vai trò của a,b,c như nhau
Giả sử a=b=5
Thay vào công thức
=> \(8c=\sqrt{\left(10+c\right)\left(10-c\right)\left(c\right)\left(c\right)}\)
=> \(64c^2=100c^2+c^4\)
=> \(c=6\)
Vậy ba cạnh của tam giác là 5,5,6

Ta có: \(\widehat B = {65^o},\widehat C = {85^o}.\)
\( \Rightarrow \widehat A = {180^o} - \left( {{{65}^o} + {{85}^o}} \right) = {30^o}.\)
Áp dụng định lí sin trong tam giác ABC, ta có:
\(\frac{{BC}}{{\sin A}} = 2R \Rightarrow BC = 2R.\sin A\)
Mà \(\widehat A = {30^o},R = 6.\)
\( \Rightarrow BC = 2.6.\sin {30^o} = 6.\)
Vậy BC = 6.