CHO tam giác ABC kéo dài cạnh AB một đoạn BD=AB và kéo dài một đoạn CE=AC.Nối DC và kéo dài DC một đoạn CM=CD .nối EB và kéo dài EB một đoạn BN=BE .chứng minh a. M,A.N thẳng hàng b. A là trung điểm của đoan thăng MN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 11 2015
Bạn tự vẽ hình nhé!
+) Xét tam giác ABN và DBE có: AB = DB; góc ABN = DBE (đối đỉnh); BN = BE
=> tam giác ABN = DBE ( c- g - c)
=> góc BDE = BAN và AN = DE
+) Tương tự, tam giác ACM = ECD ( c - g - c)
=> góc CED = CAM và DE = AM
+) Tam giác ADE có; BAC + BDE + CED = 180o
=> BAC + BAN + CAM = 180o
=> góc NAM = 180o => A; M; N thẳng hàng
Mặt khác, AN = AM (= DE)
=> A là trung điểm của MN
28 tháng 8 2021
a: Xét tứ giác ABCM có
E là trung điểm của đường chéo AC
E là trung điểm của đường chéo BM
Do đó: ABCM là hình bình hành
Suy ra: BC=AM
28 tháng 8 2021
a: Xét tứ giác ABCM có
E là trung điểm của đường chéo AC
E là trung điểm của đường chéo BM
Do đó: ABCM là hình bình hành
Suy ra: BC=AM
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
10 tháng 9 2020
Nối M với C; N với D; P với A và Q với B
Nối A với C; B với D
Ta có S(ABCD)=S(ABD)+S(BCD)=S(ABC)+S(ACD)
Xét tg ABQ và tg ABD có chung đường cao hạ từ B xuống DQ và cạnh đáy AQ=AD nên S(ABQ)=S(ABD)
Xét tg ABQ và tg BMQ có chung đường cao hạ từ Q xuống AM và cạnh đáy AB=BM nên S(ABQ)=S(BMQ)
=> S(ABQ)=S(BMQ)=S(ABD) => S(AMQ)=S(ABQ)+S(BMQ)=2xS(ABD) (1)
Chứng minh tương tự khi xét các tam giác BCD với tg CDN và tg CDN với tg DNQ => S(CNP)=2xS(BCD) (2)
Từ (1) và (2) => S(AMQ)+S(CNP)=2xS(ABD)+2xS(BCD)=2x[S(ABD)+S(BCD)]=2xS(ABCD)
Chứng minh tương tự ta sẽ có kết quả S(DPQ)+S(CMN)=2x[S(ACD)+S(ABC)]=2xS(ABCD)
S(MNPQ)=[S(AMQ)+S(CNP)]+[S(DPQ)+S(CMN)]+S(ABCD)=5xS(ABCD)=5x25=125 cm2
3 tháng 4 2023
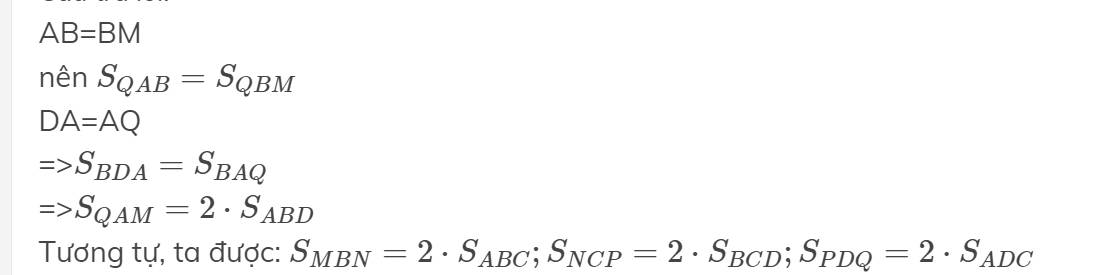
=>\(S_{MNPQ}=S_{MBN}+S_{NCP}+S_{PDQ}+S_{QMA}+S_{ABCD}\)
\(=5\cdot S_{ABCD}=5\cdot25=125\left(cm^2\right)\)