Cho hàm số \(y=mx^3-2x-5\). Tìm m để y' < 0 với mọi x?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
21 tháng 10 2021
Đường thẳng y = ( m -3 ).x + 5 đi qua A(-5;1)
=> A(-5;1) thuộc hàm số y = ( m - 3 ).x + 5
1 = ( m - 3).(-5) + 5
1 = -5m + 15 + 5
1 = -5m + 20
-5m = -19
m = 19/5
Vậy m = 19/5 thì y = ( m - 3)x + 5 đi qua A(-5;1)
31 tháng 10 2021
a) Ta có \(y=mx+m-2x=\left(m-2\right)x+m\)
Như vậy để y là hàm số bậc nhất thì \(m-2\ne0\Leftrightarrow m\ne2\)
b) Để y là hàm số nghịch biến thì \(m-2< 0\Leftrightarrow m< 2\)
c) Để y là hàm số đồng biến thì \(m-2>0\Leftrightarrow m>2\)
TA
31 tháng 7 2021
`f'(x) = x^2 - 4x+m`
`f'(x) >=0 <=>x^2-4x+m>=0`
`<=> \Delta' >=0`
`<=> 2^2-1.m>=0`
`<=> m<=4`
Vậy....
6 tháng 11 2021
a: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}-2x=x-3\\y=x-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
28 tháng 3 2023
Tọa độ giao điểm là:
2x-1=-mx-5 và y=2x-1
=>x(m+2)=-4 và y=2x-1
=>x=-4/m+2 và y=-8/m+2-1=(-8-m-2)/(m+2)=(-m-10)/(m+2)
Để x,y đối nhau thì -4-m-10=0
=>m+14=0
=>m=-14
CM
1 tháng 3 2017
Chọn D.
Phương pháp:
Sử dụng tính chất đồ thị hàm đa thức bậc ba luôn cắt trục tung và đồ hàm số y=f(|x|) luôn nhận trục tung làm trục đối xứng để suy ra x=0 luôn là một cực trị của hàm y=f(|x|)
Lập luận để suy ra hàm f(x) có hai điểm cực trị dương phân biệt thì hàm số y=f(|x|) có 5 điểm cực trị
phân biệt.
Cách giải:
Nhận thấy rằng nếu x 0 là điểm cực trị của hàm số y=f(|x|) cũng là điểm cực trị của hàm số y=f(|x|) (1)
Lại thấy vì đồ thị hàm số y=f(|x|) nhận trục Oy làm trục đối xứng mà f(x) là hàm đa thứ bậc ba nên x=0 luôn là một điểm cực trị của hàm số y=f(|x|) (2)
Từ (1) và (2) suy ra để hàm số y=f(|x|) có 5 điểm cực trị thì hàm số
1 tháng 9 2021
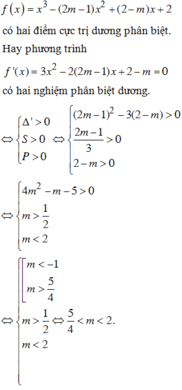
a: Thay x=1 và y=1 vào (d), ta được:
m+3=1
hay m=-2
b: Vì (d)//y=-2x+3 nên a=-2
Vậy: (d): y=-2x+b
Thay x=0 và y=-3 vào (d), ta được:
b=-3
\(y'=3mx^2-2\)
Để \(y'< 0\) \(\forall x\Rightarrow\max\limits_{x\in R}g\left(x\right)=3mx^2-2< 0\)
\(g'\left(x\right)=6mx=0\Rightarrow x=0\)
\(\Rightarrow\left\{{}\begin{matrix}m\le0\\g\left(0\right)< 0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\le0\\-2< 0\end{matrix}\right.\) \(\Rightarrow m\le0\)