Cách tính chu vi hình vuông và hình tứ giác
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)
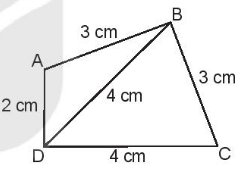
Chu vi hình tam giác ABD là:
3 + 4 + 2 = 9 (cm)
Chu vi hình tam giác BCD là:
4 + 3 + 4 = 11 (cm)
b)
Chu vi hình tứ giác ABCD là:
3 + 3 + 4 + 2 = 12 (cm)
c)
Tổng chu vi của tam giác ABD và BCD là:
9 + 11 = 20 (cm)
Tổng chu vi của tam giác ABD và BCD hơn chu vi hình tứ giác ABCD là:
20 – 12 = 8 (cm)

a)Áp dụng HTL2 vào tam giác ABC cuông tại A, đường cao AH ta có:
AH2=BH.HC=9.16=144
<=>AH=√144=12((cm)
Áp dụng định lý Pytago vào tam giác vuông BHA ta có:
BA2=AH2+BH2=122+92=225
<=>BA=√225=15(cm)
Áp dụng định lý Pytago vào tam giác vuông CHA ta có:
CA2=AH2+CH2=122+162=20(cm)
Vậy AB=15cm,AC=20cm,AH=12cm

- Tên các hình đã học: hình tứ giác, hình tam giác, hình chữ nhật, hình vuông.
- Cách tính chu vi
+ hình tam giác: độ dài 3 cạnh tam giác cộng lại với nhau (cùng một đơn vị đo).
+ hình tứ giác: độ dài 4 cạnh tam giác cộng lại với nhau (cùng một đơn vị đo).
+ hình chữ nhật: chiều dài cộng chiều rộng nhân với 2 (cùng một đơn vị đo).
+ hình vuông: độ dài một cạnh nhân với 4.
- Cách tính diện tích
+ hình chữ nhật: chiều dài nhân với chiều rộng (cùng một đơn vị đo).
+ hình vuông: độ dài một cạnh nhân với chính nó.
- Tên các đơn vị đo
+ độ dài: km, m, dm, cm, mm.
+ khối lượng: g, kg.
+ dung tích: ml , l.
+ diện tích: \(km^2,m^2,dm^2,cm^2,mm^2\).

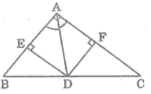

Nên tứ giác AFDE là hình vuông
* Vì DE ⊥ AB, AC ⊥ AB nên DE // AC
Theo định lí Ta-lét ta có: CD/BC = AE/AB

chu vi hình vuông lấy 1 cạnh nhân 4