Tập nghiệm của bất phương trình: (16-x2)\(\sqrt{x-3}\) ≤ 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn A.
Tam thức f(x) = x 2 + x - 12 có a = 1 > 0 và có hai nghiệm x 1 = -4; x 2 = 3
(f(x) trái dấu với hệ số a).
Suy ra x 2 + x - 12 < 0 ⇔ -4 < x < 3
Vậy tập nghiệm của bất phương trình là S = (-4;3).

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

Chọn B.
Ta có:
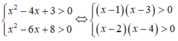
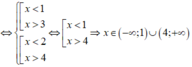
Vậy tập nghiệm của bất phương trình là S = ( - ∞ ;1) ∪ (4; + ∞ ).

Đáp án: A
Ta có bảng xét dấu:

Dựa vào bảng xét dấu ta thấy tập nghiệm của bất phương trình là: (- ∞ ;1) ∪ (4;+ ∞ )


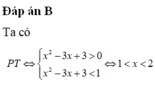
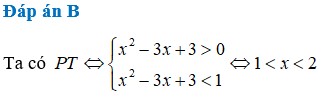
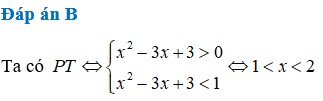
\(\left(16-x^2\right)\sqrt{x-3}\le0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3\ge0\\16-x^2\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge3\\x\in(-\infty;-4]\cup[4;+\infty)\end{matrix}\right.\)
\(\Leftrightarrow\left\{3\right\}\cup[4;+\infty)\)