Cho các số nguyên x,y thoả mãn 5x - 2y = 1. Tìm giá trị nhỏ nhất của biểu thức T = 3 | x | + 5 | y |
Giải thích đầy đủ nha mn giúp mình mai thi HKII rùi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
1
DD
Đoàn Đức Hà
Giáo viên
21 tháng 7 2021
\(5x-2y=1\)(1)
Có \(\left(5,2\right)=1\)là ước của \(1\)nên phương trình có vô số nghiệm.
Thấy \(\left(1,2\right)\)là một nghiệm của (1) nên nghiệm tổng quát của (1) là:
\(\hept{\begin{cases}x=1+\frac{-2}{1}t=1-2t\\y=2+\frac{5}{1}t=2+5t\end{cases}}\left(t\inℤ\right)\)
\(P=3x+5y=3\left(1-2t\right)+5\left(2+5t\right)=13+19t\)
Dễ thấy \(P\)không có giá trị nhỏ nhất do \(t\inℤ\).
Nếu đổi điều kiện là \(x,y\)là các số tự nhiên.
Ta có: \(\hept{\begin{cases}x=1+\frac{-2}{1}t=1-2t\\y=2+\frac{5}{1}t=2+5t\end{cases}}\left(t\inℤ\right)\)suy ra \(\hept{\begin{cases}1-2t\ge0\\2+5t\ge0\end{cases}}\Leftrightarrow\frac{-2}{5}\le t\le\frac{1}{2}\)suy ra \(t=0\).
Khi đó \(P=3.1+5.2=13\).
CM
17 tháng 4 2017
Đáp án C.
Ta có:
G T ⇔ 5 x + 2 y + x + 2 y − 3 − x − 2 y = 5 x y − 1 − 3 1 − x y + x y − 1.
Xét hàm số
f t = 5 t + t − 3 − t ⇒ f t = 5 t ln 5 + 1 + 3 − t ln 3 > 0 ∀ t ∈ ℝ
Do đó hàm số đồng biến trên ℝ suy ra f x + 2 y = f x y − 1 ⇔ x + 2 y = x y − 1
⇔ x = 2 y + 1 y − 1 ⇒ T = 2 y + 1 y − 1 + y . Do x > 0 ⇒ y > 1
Ta có: T = 2 + y + 3 y − 1 = 3 + y − 1 + 3 y − 1 ≥ 3 + 2 3 .
CM
12 tháng 11 2019
Đáp án C.
Ta có: GT
<=> 5x+2y + x + 2y – 3–x–2y = 5xy–1 – 31–xy + xy – 1.
X é t h à m s ố f t = 5 t + t - 3 - t
⇒ f t = 5 t ln 5 + 1 + 3 - t ln 3 > 0 ∀ t ∈ ℝ
Do đó hàm số đồng biến trên ℝ suy ra
f(x+2y) = f(xy – 1) <=> x+ 2y = xy – 1
⇔ x = 2 y + 1 y - 1 ⇒ T = 2 y + 1 y - 1 + y .
Do x > 0 => y > 1.
Ta có:
T = 2 + y + 3 y - 1 = 3 + y - 1 + 3 y - 1 ≥ 3 + 2 3 .
CM
26 tháng 4 2018
Đáp án B.
Từ giả thiết, suy ra
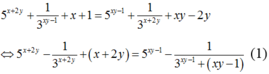
Xét hàm số f ( t ) = 5 t - 1 3 t + t trên ℝ .
Đạo hàm f ' ( t ) = 5 t . ln 5 - ln 3 3 t + 1 > 0 , ∀ t ∈ ℝ ⇒ hàm số f ( t ) luôn đồng biến trên ℝ .
Suy ra
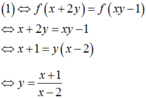
Do y > 0 nên x + 1 x - 2 > 0 ⇔ [ x > 2 x < - 1 . Mà x > 0 nên x > 2 .
Từ đó T = x + y = x + x + 1 x - 2 . Xét hàm số g ( x ) = x + x + 1 x - 2 trên 2 ; + ∞ .
Đạo hàm
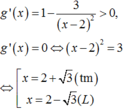
Lập bảng biến thiên của hàm số trên 2 ; + ∞ , ta thấy min g ( x ) = g ( 2 + 3 ) = 3 + 2 3 .
Vậy T m i n = 3 + 2 3 khi x = 2 + 3 và x = 1 + 3 .
