Tìm nghiệm nguyên của phương trình sau:
1992x1993 + 1993y1994 = 1995
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NL
1
TA
1 tháng 2 2021
\(2x+3y=7 \\ \Leftrightarrow x=\dfrac{-7-3y}{2} \)
PT có nghiệm nguyên \(\Leftrightarrow -7-3y \vdots 2 \\ \Leftrightarrow (-7-3y \in Ư(2) \\ \Leftrightarrow -7-3y \in {-2;2;-1;1} \\ \Leftrightarrow y \in {\dfrac{-5}{3} (L) ; -3(TM); -2(TM) ; \dfrac{-8}{3} (L)} \)
- Với \(y=-3\) có: \(x=1\).
- Với \(y=-2\) có: \(x=\dfrac{-1}{2} (L)\)
Vậy \((x;y)=(-3;1)\) là nghiệm nguyên duy nhất của phương trình.
NX
1
6 tháng 8 2023
Xét \(y=0\Rightarrow x=\pm8\)
Với \(y\ge1\), ta thấy \(x⋮6\) và \(y⋮2\) (vì nếu \(y\) lẻ thì \(3^y\) chia 4 dư 3, vô lí)
\(x=3k,y=2l\left(k,l\inℤ,l\ge2\right)\) (nếu \(l=1\) thì \(y=2\Rightarrow x^2=72\), vô lí)
pt đã cho trở thành \(k^2=3^{2l-2}+7\)
\(\Leftrightarrow k^2-\left(3^{l-1}\right)^2=7\)
\(\Leftrightarrow\left(k+3^{l-1}\right)\left(k-3^{l-1}\right)=7\)
Do \(k+3^{l-1}>k-3^{l-1}\) nên ta xét 2TH
TH1: \(\left\{{}\begin{matrix}k+3^{l-1}=7\\k-3^{l-1}=1\end{matrix}\right.\). Cộng theo vế \(\Rightarrow2k=8\Rightarrow k=4\Rightarrow x=3k=12\) \(\Rightarrow3^y=x^2-63=144-63=81\Rightarrow y=4\)
Vậy ta tìm được cặp \(\left(x,y\right)=\left(12,4\right)\), thử lại thấy thỏa mãn.
TH2: \(\left\{{}\begin{matrix}k+3^{l-1}=-1\\k-3^{l-1}=-7\end{matrix}\right.\)
Cộng theo vế \(\Rightarrow2k=-8\Rightarrow k=-4\Rightarrow x=-12\)
\(\Rightarrow3^y=x^2-63=144-63=81\Rightarrow y=4\)
Vậy ta tìm được thêm cặp số \(\left(x;y\right)=\left(-12;4\right)\). Như vậy, pt đã cho có các nghiệm nguyên \(\left(x;y\right)\in\left\{\left(\pm8;0\right);\left(\pm12;4\right)\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 2 2022
Em tham khảo ở đây:
Tìm nghiệm nguyên dương của phương trình sau: \(3^x-2^y=1\) - Hoc24
KN
6 tháng 3 2020
\(2xy+6x-y=2020\)
\(\Leftrightarrow2x\left(y+3\right)-\left(y+3\right)=2017\)
\(\Leftrightarrow\left(2x-1\right)\left(y+3\right)=2017=2017.1=1.2017\)
\(=\left(-2017\right).\left(-1\right)=\left(-1\right).\left(-2017\right)\)
Lập bảng:
| \(2x-1\) | \(2017\) | \(1\) | \(-1\) | \(-2017\) |
| \(y+3\) | \(1\) | \(2017\) | \(-2017\) | \(-1\) |
| \(x\) | \(1009\) | \(1\) | \(0\) | \(-1008\) |
| \(y\) | \(-2\) | \(2014\) | \(-2020\) | \(-4\) |
Vậy phương trình có 4 cặp nghiệm nguyên \(\left(1009;-2\right);\left(1;2014\right);\left(0;-2020\right);\left(-1008;-4\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 1 2022
- Với \(x=1\Rightarrow y=1\)
- Với \(x>1\Rightarrow y>1\)
\(\Rightarrow3^x=2^y+1\)
Do \(y>1\Rightarrow2^y⋮4\Rightarrow2^y+1\equiv1\left(mod4\right)\) \(\Rightarrow3^x\equiv1\left(mod4\right)\)
Nếu \(x=2k+1\Rightarrow3^x=3^{2k+1}=3.9^k\equiv3\left(mod4\right)\) (ktm)
\(\Rightarrow x=2k\Rightarrow3^{2k}-1=2^y\)
\(\Rightarrow\left(3^k-1\right)\left(3^k+1\right)=2^y\)
\(\Rightarrow\left\{{}\begin{matrix}3^k-1=2^a\\3^k+1=2^b\end{matrix}\right.\) với \(b>a\Rightarrow2^b-2^a=2\)
\(\Rightarrow2^a\cdot\left(2^{b-a}-1\right)=2\Rightarrow2^a=2\Rightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\)
\(\Rightarrow3^k-1=2\Rightarrow k=1\Rightarrow x=2\Rightarrow y=3\)
Vậy \(\left(x;y\right)=\left(1;1\right);\left(2;3\right)\)
V
2
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 9 2021
\(\Leftrightarrow4x^2-4xy+y^2=16-3y^2\)
\(\Leftrightarrow16-3y^2=\left(2x-y\right)^2\ge0\)
\(\Rightarrow y^2\le\dfrac{16}{3}\)
\(\Rightarrow y^2=\left\{1;4\right\}\)
\(\Rightarrow\left[{}\begin{matrix}y=1\\y=2\end{matrix}\right.\)
- Với \(y=1\Rightarrow4x^2-4x+4=16\Leftrightarrow x^2-x-3=0\) (ko có x nguyên thỏa mãn)
- Với \(y=2\Rightarrow4x^2-8x=0\Rightarrow x=2\)
Vậy \(\left(x;y\right)=\left(2;2\right)\)
PT
1
CM
15 tháng 1 2018
Ta có: x(x3 - x + 6) > 9
⇔ x4 - x2 + 6x - 9 > 0
⇔ f(x) > 0
thấy f(x) > 0 khi
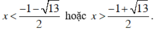
Vậy tập nghiệm của bất phương trình là
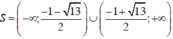
Do \(1992.x^{1993}\) luôn chẵn, mà 1995 lẻ \(\Rightarrow1993.y^{1994}\) lẻ
\(\Rightarrow y\) lẻ \(\Rightarrow y^{997}\) lẻ\(\Rightarrow\)đặt \(y^{997}=2k+1\)
Phương trình trở thành:
\(1992.x^{1993}+1993\left(2k+1\right)^2=1995\)
\(\Leftrightarrow1992.x^{1993}+1993\left(4k^2+4k\right)+1993=1995\)
\(\Leftrightarrow4\left(498x^{1993}+1993\left(k^2+k\right)\right)=1995-1993=2\)
Vế trái chia hết cho 4, vế phải ko chia hết cho 4 \(\Rightarrow\) pt vô nghiệm
Vậy ko có cặp số nguyên nào thỏa mãn