Question

[senorita]

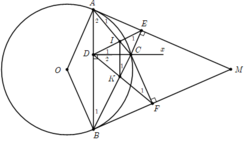
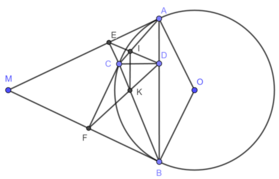
Từ điểm M nằm ngoài đường tròn (O) kẻ hai tiếp tuyến MA,MB với đường tròn (A, B là các tiếp điểm). Lấy điểm C trên cung nhỏ AB( C không trùng với A,B) . Từ điểm C kẻ CD vuông góc với AB, CE vuông góc với MA, CF vuông góc với MB (D thuộc AB, E thuộc MA, F thuộc MB). Gọi I là giao điểm của AC và DE, K là giao điểm của BC và DF. CMR

1. ADEC nội tiếp (đã làm)

2. tam giác CDE đồng dạng tam giác CFD (đã làm)

3. Tia đối CD là phân giác góc ECF

4. Đường thẳng IK song song với AB (đã làm)

Answer 1

[Nguyễn Linh Chi]

a) Ta có CD vuông AB => \(\widehat{CDA}=90^o\)

CE vuông AM => \(\widehat{CEA}=90^o\)

Xét tứ giác ADCE có :\(\widehat{CDA}+\widehat{CEA}=90^o+90^o=180^o\)

=> Tứ giác ADCE nội tiếp

b) Tương tự ta chứng minh được tứ giác CDBF nội tiếp

Tứ giác ADCE nội tiếp => \(\widehat{CDE}=\widehat{CAE}\)( cùng chắn cung CE)

 Tứ giác CDBF nội tiếp => \(\widehat{CFD}=\widehat{CBD}\)( cùng chắn cung DC)

Mà \(\widehat{CBD}=\widehat{CAE}\)( cùng chắn cung AC của đường tròn (O))

=> \(\widehat{CDE}=\widehat{CFD}\)

Tương tự như trên ta chứng minh được : \(\widehat{DEC}=\widehat{DAC}=\widehat{CBF}=\widehat{FDC}\)

Xét tam giác CDE  và tam giác CFD có: 

\(\widehat{CDE}=\widehat{CFD}\)

\(\widehat{DEC}=\widehat{FDC}\)

=> \(\Delta CDE=\Delta CFD\)

3) Gọi Cx là tia đối của ta CD

Nối OM. Dễ dàng chứng minh được: OM vuông AB, \(\widehat{AOM}=\widehat{BOM}\)(1)

Ta có: Cx//OM ( cùng vuông góc với AB), CE//OA ( cùng vuông với AM)

=> \(\widehat{AOM}=\widehat{ECx}\)(2)

Cx// OM, CF//OB ( cùng vuông với BM)

=> \(\widehat{BOM}=\widehat{FCx}\)(3)

Từ (1), (2), (3), 

=> \(\widehat{ECx}=\widehat{FCx}\)

=> Cx là phân giác góc ECF

4. Ở câu 2 Ta đã chứng minh : \(\widehat{CDE}=\widehat{CBD}\Rightarrow90^o=\widehat{DCB}+\widehat{CBD}=\widehat{CDE}+\widehat{DCB}=\widehat{CDI}+\widehat{DCK}\)

Tương tự như trên chứng minh được: \(\widehat{CDK}+\widehat{ICD}=90^o\)

Xét tứ giác IDKC có: \(\widehat{IDK}+\widehat{ICK}=\widehat{IDC}+\widehat{CDK}+\widehat{ICD}+\widehat{DCK}=\left(\widehat{IDC}+\widehat{DCK}\right)+\left(\widehat{CDK}+\widehat{ICD}\right)\)

\(=90^o+90^o=180^o\)

=> Tứ giác IDKC nội tiếp

=> \(\widehat{IKC}=\widehat{IDC}=\widehat{DBC}\)

=> IK//AB ( 2 góc so le trong)