Giúp mùi vs ạ cần gấp bây h trong 15p ạ😓
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 1 2022
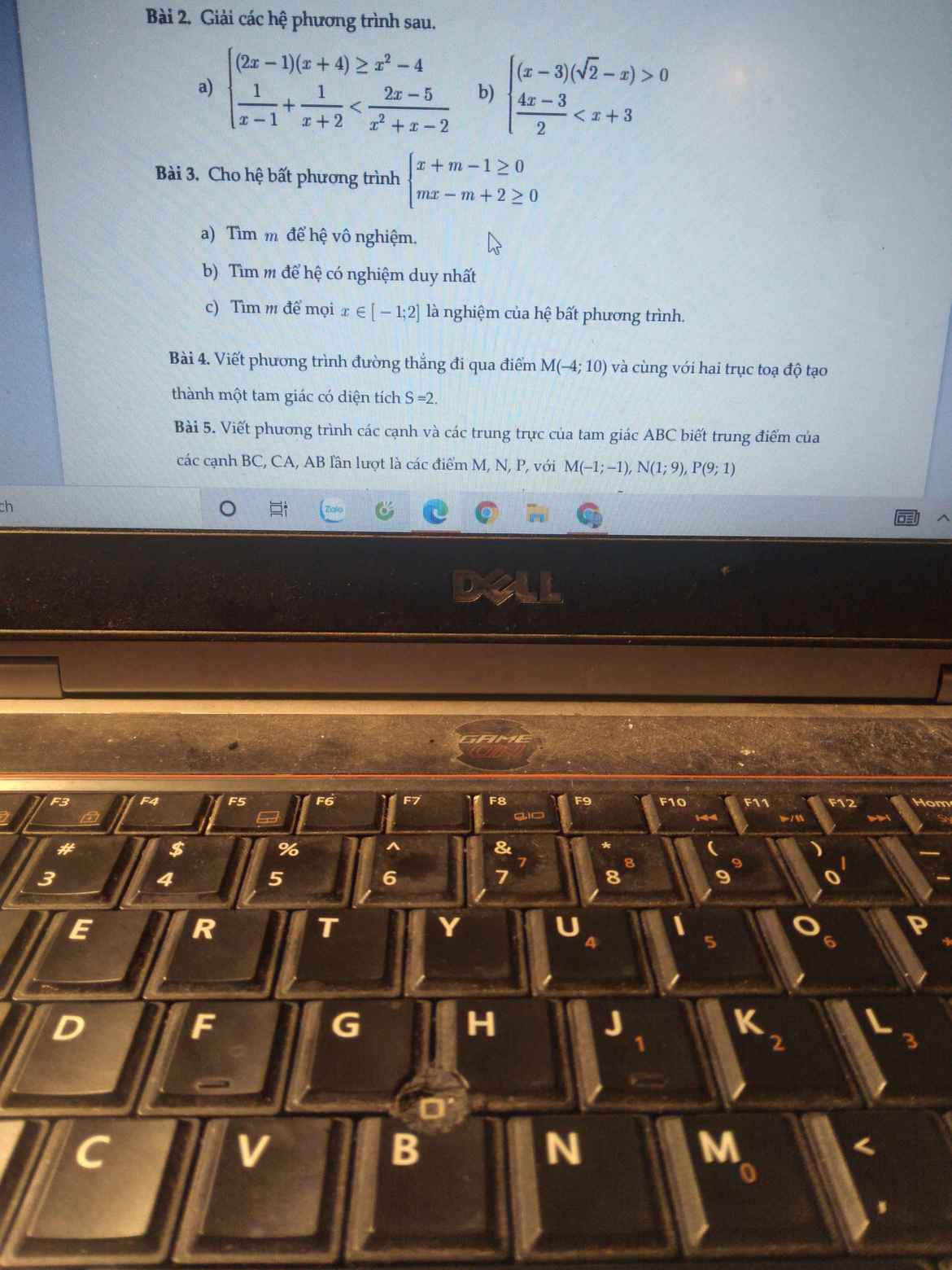
C3: Hệ bpt trở thành: \(\left\{{}\begin{matrix}x\ge1-m\\mx\ge2-m\end{matrix}\right.\)
a, Để hệ phương trình vô nghiệm thì \(m=0\)
b, Để hệ có nghiệm duy nhất thì \(\left\{{}\begin{matrix}m\ne0\\\dfrac{m-2}{m}=1-m\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}m\ne0\\m=\pm\sqrt{2}\end{matrix}\right.\) \(\Leftrightarrow\) \(m=\pm\sqrt{2}\)
c, \(x\in\left[-1;2\right]\) \(\Leftrightarrow\) \(-1\le x\le2\)
Để mọi \(x\in\left[-1;2\right]\) là nghiệm của hệ bpt trên thì
\(\left\{{}\begin{matrix}-1\le1-m\le2\\-1\le\dfrac{2-m}{m}\le2\end{matrix}\right.\) với \(m\ne0\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}2\ge m\ge-1\\m\ge\dfrac{2}{3}\end{matrix}\right.\) \(\left(m\ne0\right)\)
\(\Leftrightarrow\) \(2\ge m\ge\dfrac{2}{3}\)
Vậy \(m\in\left[\dfrac{2}{3};2\right]\) thì mọi \(x\in\left[-1;2\right]\) là nghiệm của hệ bpt
Chúc bn học tốt!
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 3 2023
27.
Bán kính mặt cầu ngoại tiếp tứ diện vuông được tính bằng:
\(R=\sqrt{\dfrac{OA^2+OB^2+OC^2}{4}}=\sqrt{\dfrac{1^2+2^2+3^2}{4}}=\dfrac{\sqrt{14}}{2}\)
28.
Từ giả thiết suy ra \(A\left(2;2;2\right)\)
Gọi điểm thuộc mặt Oxz có tọa độ dạng \(D\left(x;0;z\right)\)
\(\Rightarrow\overrightarrow{AD}=\left(x-2;-2;z-2\right)\)
\(\overrightarrow{BD}=\left(x+2;-2;z\right)\) ; \(\overrightarrow{CD}=\left(x-4;-1;z+1\right)\)
D cách đều A, B, C \(\Rightarrow\left\{{}\begin{matrix}AD=BD\\AD=CD\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left(x-2\right)^2+4+\left(z-2\right)^2=\left(x+2\right)^2+4+z^2\\\left(x-2\right)^2+4+\left(z-2\right)^2=\left(x-4\right)^2+1+\left(z+1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+z=1\\2x-3z=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}z=-\dfrac{1}{2}\\x=\dfrac{3}{4}\end{matrix}\right.\)
\(\Rightarrow P\left(\dfrac{3}{4};0;-\dfrac{1}{2}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 3 2023
29.
Do tâm I mặt cầu thuộc Oz nên tọa độ có dạng: \(I\left(0;0;z\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AI}=\left(-3;1;z-2\right)\\\overrightarrow{BI}=\left(-1;-1;z+2\right)\end{matrix}\right.\)
Mặt cầu qua A, B nên \(AI=BI\)
\(\Leftrightarrow3^2+1^2+\left(z-2\right)^2=1^2+1^2+\left(z+2\right)^2\)
\(\Leftrightarrow8z=8\Rightarrow z=1\)
\(\Rightarrow I\left(0;0;1\right)\Rightarrow R=IB=\sqrt{1^2+1^1+3^2}=\sqrt{11}\)
Phương trình mặt cầu:
\(x^2+y^2+\left(z-1\right)^2=11\)
DA
3
DT
27 tháng 1 2023
Câu 1: Tác phẩm "Cô bé bán diêm"
Tác giả: An - đéc - xen.
Câu 2: ngôi thứ 3.
Câu 3:
Chi tiết: Ngọn lửa lúc đầu xanh lam ... vui mắt.
+ que diêm sáng rực như than hồng.
+ Chà! Ánh sáng kì dị làm sao.
Ý nghĩa hình ảnh ngọn lửa:
+ thể hiện lên thứ sưởi ấm trái tim, tâm hồn, thể xác cô gái nghèo bé nhỏ giữa đêm Noel lạnh giá.
+ thể hiện tinh thần nhân đạo của tác giả.
Câu 4:
- Em cần:
+ Quan tâm tới bạn, cùng bạn học tập, giúp đỡ việc học của bạn.
+ Ý kiến với thầy cô, nhà trường giúp đỡ bạn.
Đ 2:
a)
Nhiều nhân dân chăm chỉ
Đồng bào ta
Những cái bàn ghế.
b)
Những tiếng hát.
Các lần múa.
Đang chạy
c)
Hơi xanh.
Còn nhạt quá.
Ngọt lắm.
20 tháng 10 2021
a: Thay x=2 vào y=2x-1, ta được:
y=4-1=3
Thay x=2 và y=3 vào y=ax-4, ta được:
2a-4=3
hay \(a=\dfrac{7}{2}\)
83
2
S
16 tháng 1 2022
PTHH : 2Al + 6HCl --> 2AlCl3 + 3H2 ↑ (1)
nAlCl3 = \(\dfrac{m}{M}=\dfrac{13,35}{27+35,5.3}=0.1\left(mol\right)\)
Từ (1) => nHCl = 2nH2 = 0.2 (mol)
=> mHCl = n.M = 0.2 x 36.5 = 7.3 (g)
16 tháng 1 2022
\(PTHH:2Al+6HCl\rightarrow2AlCl_3+3H_2\\ n_{AlCl_3}=\dfrac{m}{M}=\dfrac{13,35}{133,5}=0,1\left(mol\right)\\ Theo.PTHH:n_{HCl}=3.n_{AlCl_3}=3.0,1=0,3\left(mol\right)\\ m_{HCl}=n.M=0,3.36,5=10,95\left(g\right)\)
DT
Đỗ Thanh Hải
CTVVIP
20 tháng 7 2021
3 B
4 C
5 C
6 C
7D
8 C
9 A
10 A
11 B
12 A
13 D
14 D
15 B
16 A
17 C
18 A
19 B
20 B
21 C
22 B
23 C
24 B
25 A
26 C
8 tháng 5 2023
"Theo điều học mà làm" có nghĩa là biến kiến thức trong sách vở thành hành động thực tế. Chúng ta cần làm vậy bởi:
- Việc áp dụng kiến thức vào công việc giúp chúng ta khắc sâu kiến thức và những tri thức sách vở không còn là thứ nằm trên trang giấy mà được áp dụng vào thực tế
- Nếu chỉ có học mà không làm ta sẽ thiếu hụt kinh nghiệm cá nhân và vốn sống thực tế => sẽ không được trọng dụng trong tương lai và khó phát huy hoàn toàn tài năng của mình