Trả lời giúp: (2x + 1)3 - (2x + 1)(4x2 - 2x + 1) = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 12 2021
\(a,\Leftrightarrow9x^2=-36\Leftrightarrow x\in\varnothing\\ b,\Leftrightarrow3\left(x+4\right)-x\left(x+4\right)=0\\ \Leftrightarrow\left(3-x\right)\left(x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=-4\end{matrix}\right.\\ c,\Leftrightarrow2x^2-x-2x^2+3x+2=0\\ \Leftrightarrow2x=-2\Leftrightarrow x=-1\\ d,\Leftrightarrow\left(2x-3-2x\right)\left(2x-3+2x\right)=0\\ \Leftrightarrow-3\left(4x-3\right)=0\\ \Leftrightarrow x=\dfrac{3}{4}\\ e,\Leftrightarrow\dfrac{1}{3}x\left(x-9\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=9\end{matrix}\right.\\ f,\Leftrightarrow x^2\left(x-1\right)-\left(x-1\right)=0\\ \Leftrightarrow\left(x^2-1\right)\left(x-1\right)=0\\ \Leftrightarrow\left(x-1\right)^2\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
CM
10 tháng 2 2018
a) 2(x + 3)(x – 4) = (2x – 1)(x + 2) – 27
⇔ 2(x2 – 4x + 3x – 12) = 2x2 + 4x – x – 2 – 27
⇔ 2x2 – 2x – 24 = 2x2 + 3x – 29
⇔ -2x – 3x = 24 – 29
⇔ - 5x = - 5 ⇔ x = -5/-5 ⇔ x = 1
Tập nghiệm của phương trình : S = {1}
b) x2 – 4 – (x + 5)(2 – x) = 0
⇔ x2 – 4 + (x + 5)(x – 2) = 0 ⇔ (x – 2)(x + 2 + x + 5) = 0
⇔ (x – 2)(2x + 7) = 0 ⇔ x – 2 = 0 hoặc 2x + 7 = 0
⇔ x = 2 hoặc x = -7/2
Tập nghiệm của phương trình: S = {2; -7/2 }
c) ĐKXĐ : x – 2 ≠ 0 và x + 2 ≠ 0 (khi đó : x2 – 4 = (x – 2)(x + 2) ≠ 0)
⇔ x ≠ 2 và x ≠ -2
Quy đồng mẫu thức hai vế :
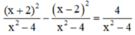
Khử mẫu, ta được : x2 + 4x + 4 – x2 + 4x – 4 = 4
⇔ 8x = 4 ⇔ x = 1/2( thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {1/2}
d) ĐKXĐ : x – 1 ≠ 0 và x + 3 ≠ 0 (khi đó : x2 + 2x – 3 = (x – 1)(x + 3) ≠ 0)
⇔ x ≠ 1 và x ≠ -3
Quy đồng mẫu thức hai vế :
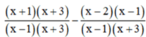
Khử mẫu, ta được : x2 + 3x + x + 3 – x2 + x – 2x + 2 + 4 = 0
⇔ 3x = -9 ⇔ x = -3 (không thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = ∅
PN
15 tháng 5 2021
\(2\left(x+3\right)\left(x-4\right)=\left(2x-1\right)\left(x+2\right)-27\)
\(< =>2\left(x^2-x-12\right)=2x^2+3x-2-27\)
\(< =>2x^2-2x-24=2x^2+3x-2-27\)
\(< =>5x=-24+29=5\)
\(< =>x=\frac{5}{5}=1\)
PT
1
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 12 2020
a.
\(\left(4x^2+4x+1\right)-y^2=\left(2x+1\right)^2-y^2=\left(2x+1-y\right)\left(2x+1+y\right)\)
b.
\(\Leftrightarrow2x^2+2x-x-1-2x^2-3x+1=0\)
\(\Leftrightarrow-2x=0\)
\(\Leftrightarrow x=0\)
LU
1
26 tháng 2 2021
=>\(\orbr{\begin{cases}x+\frac{1}{2}=0\\\frac{2}{3}-2x=0\end{cases}}\)
+, x+\(\frac{1}{2}\)=0 +,\(\frac{2}{3}-2x=0\)
x=\(-\frac{1}{2}\) =>\(\frac{2}{3}=2x\)
=>\(x=\frac{1}{3}\)
Vậy........
VD
18 tháng 3 2022
\(a,x\left(1-2x\right)-2=\left(2x-3\right)\left(1-x\right)\\ \Leftrightarrow x-2x^2-2=2x-3-2x^2+3x\\ \Leftrightarrow2x-3-2x^2+3x-x+2x^2+2=0\)
\(\Leftrightarrow4x-1=0\\ \Leftrightarrow x=\dfrac{1}{4}\)
\(b,2x\left(x-2\right)+5x-10=0\\ \Leftrightarrow2x\left(x-2\right)+5\left(x-2\right)=0\\ \Leftrightarrow\left(x-2\right)\left(2x+5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{5}{2}\end{matrix}\right.\)
BV
3
24 tháng 5 2018
=> \(x^4+x^4-\left(x^5+x^2\right)-2x=1\)
=> \(x^5-x^5-x^2-2x=1\)
=> \(0-x.\left(x+2\right)=1\)
=> \(x.\left(x+2\right)=-1\)
Ta có bảng:
| \(x\) | \(1\) | \(-1\) |
| \(x+2\) | \(-1\) | \(1\) |
=>
| \(x\) | \(1\) | \(-1\) |
| \(x\) | \(-3\) | \(-1\) |
Vậy x = 1;-1;-3
24 tháng 5 2018
\(x^4+3x^3-x^2-x^3-3x^2+x-x^2-3x+1.\)
\(\left(x^4-x^3-x^2\right)+3\left(x^3-x^2-x\right)-\left(x^2-x-1\right)=0\)
\(x^2\left(x^2-x-1\right)+3x\left(x^2-x-1\right)-\left(x^2-x-1\right)=0\)
\(\left(x^2-x-1\right)\left(x^2+3x-1\right)=0\)
đến đây dùng denta
\(x^2-x-1=0\Leftrightarrow\Delta=b^2-4ac=1+4=5>0\)
vậy pt có 2 nghiệm phân biệt
\(x_1=\frac{-b+\sqrt{\Delta}}{2a}=\frac{1+\sqrt{5}}{2}\) " 1)
\(x_2=\frac{1-\sqrt{5}}{2}\) (2)
\(x^2+3x-1=0\)
áp dụng denta ta có \(\Delta=b^2-4ac=9+4=13>0\)
vậy pt có 2 nghiệm phân biệt
\(x_3=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-3+\sqrt{13}}{2}\) (3)
\(x_4=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-3-\sqrt{13}}{2}\) (4)
gom hết lại rồi kl nghiệm của pt là ....................
CM
3 tháng 10 2018
Ta có:
8 x 3 - 1 = 2 x 3 - 1 3 = 2 x - 1 . 4 x 2 + 2 x + 1 = - 1 - 2 x . 4 x 2 + 2 x + 1
Do đó, ( 8 x 3 - 1 : 1 - 2 x = - 4 x 2 + 2 x + 1 = - 4 x 2 - 2 x - 1
Chọn B. - 4 x 2 - 2 x - 1
14 tháng 10 2021
\(a,=x^2-4-x^2-2x-1=-2x-5\\ b,=8x^3-1-8x^3-1=-2\\ 3,\\ a,\Rightarrow x^3+8-x^3+2x=15\\ \Rightarrow2x=7\Rightarrow x=\dfrac{7}{2}\\ b,\Rightarrow x^3-3x^2+3x-1-x^3+3x^2+4x=13\\ \Rightarrow7x=14\Rightarrow x=2\)
14 tháng 10 2021
Bài 2:
a) \(=x^2-4-x^2-2x-1=-2x-5\)
b) \(=8x^3-1-8x^3-1=-2\)
Bài 3:
a) \(\Rightarrow x^3+8-x^3+2x=15\)
\(\Rightarrow2x=7\Rightarrow x=\dfrac{7}{2}\)
b) \(\Rightarrow x^3-3x^2+3x-1-x^3+3x^2+4x=13\)
\(\Rightarrow7x=14\Rightarrow x=2\)
1r443
(2x+1)^3-(2x+1)(4x^2-2x+1)=[(2x+1).(4x^2-2x+1)]-[(2x+1).(4x^2-2x+1)]
=0
=>(2x+1)^3-(2x+1).(4x^2-2x+1)=0