Giải phương trình: x4 - 8x3 + 11x2 - 8x + 1 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 8 2021
Ta có: \(x^4-8x^3+21x^2-24x+9=0\)
\(\Leftrightarrow x^4-5x^3+3x^2-3x^3+15x^2-9x+3x^2-5x+9=0\)
\(\Leftrightarrow\left(x^2-5x+3\right)\left(x^2-3x+3\right)=0\)
\(\Leftrightarrow x^2-5x+3=0\)
\(\text{Δ}=\left(-5\right)^2-4\cdot1\cdot3=25-12=13\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{5-\sqrt{13}}{2}\\x_2=\dfrac{5+\sqrt{13}}{2}\end{matrix}\right.\)
CM
20 tháng 2 2019
Ta có: 3 x 2 + 2 x + 4 = 8 x 3 + 12 x 2 + 8 x + 1 3 x 2 + 2 x + 5 = ( 2 x + 1 ) 3 + 2 x + 1 3 x 2 + 2 x + 5 (1)
Dễ thấy 3 x 2 + 2 x + 4 > 0 với mọi x. Đặt u = 3 x 2 + 2 x + 4 v = 2 x + 1 .
Ta có: ( 1 ) ⇔ u = v 3 + v u 2 + 1 ⇔ u 3 + u = v 3 + v ⇔ ( u − v ) ( u 2 + u v + v 2 + 1 ) = 0 ⇔ u = v
(Vì u 2 + u v + v 2 + 1 = u + v 2 2 + 3 4 v 2 + 1 > 0 )
u = v ⇔ 3 x 2 + 2 x + 4 = 2 x + 1 ⇒ 3 x 2 + 2 x + 4 = 4 x 2 + 4 x + 1 x 2 − 2 x − 3 = 0 ⇒ x = 3 h o a c x = − 1.
Thử lại, ta nhận x= 3
CM
10 tháng 10 2019
a) Cách 1: Khai triển HĐT rút gọn được 3 x 2 + 6x + 7 = 0
Vì (3( x 2 + 2x + 1) + 4 < 0 với mọi x nên giải được x ∈ ∅
Cách 2. Chuyển vế đưa về ( x + 3 ) 3 = ( x - 1 ) 3 Û x + 3 = x - 1
Từ đó tìm được x ∈ ∅
b) Đặt x 2 = t với t ≥ 0 ta được t 2 + t - 2 = 0
Giải ra ta được t = 1 (TM) hoặc t = -2 (KTM)
Từ đó tìm được x = ± 1
c) Biến đổi được 
d) Biến đổi về dạng x(x - 2) (x - 4) = 0. Tìm được x ∈ {0; 2; 4}
CM
5 tháng 11 2018
x4 + 5x2 + 1 = 0 (1)
Đặt x2 = t, t > 0.
(1) trở thành: t2 + 5t + 1 = 0 (2)
Giải (2):
Có a = 1; b = 5; c = 1
⇒ Δ = 52 – 4.1.1 = 21 > 0
⇒ Phương trình có hai nghiệm:
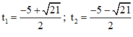
Cả hai nghiệm đều < 0 nên không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
CM
19 tháng 1 2019
Ta thấy x = 1 không phải nghiệm của phương trình nên nhân 2 vế của phương trình với x - 1 ta có:
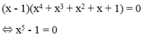
⇔ x = 1(KTM)
Vậy phương trình đã cho vô nghiệm.
PT
1
CM
16 tháng 4 2019
1) x 4 + m x 2 - m - 1 = 0
a) Khi m = 2, phương trình trở thành: x 4 + 2 x 2 – 3 = 0
Đặt x 2 = t (t ≥ 0). Khi đó ta có phương trình: t 2 + 2t - 3 = 0
⇒ Phương trình có nghiệm t = 1 và t = -3 (do phương trình có dạng a + b + c = 0)
Do t ≥ 0 nên t = 1 ⇒ x 2 = 1 ⇒ x = ±1
AH
Akai Haruma
Giáo viên
16 tháng 12 2021
Bài 1:
$2xy=(x+y)^2-(x^2+y^2)=4^2-10=6\Rightarrow xy=3$
$M=x^6+y^6=(x^3+y^3)^2-2x^3y^3$
$=[(x+y)^3-3xy(x+y)]^2-2(xy)^3=(4^3-3.3.4)^2-2.3^3=730$
AH
Akai Haruma
Giáo viên
16 tháng 12 2021
Bài 2:
$8x^3-32y-32x^2y+8x=0$
$\Leftrightarrow (8x^3+8x)-(32y+32x^2y)=0$
$\Leftrightarrow 8x(x^2+1)-32y(1+x^2)=0$
$\Leftrightarrow (8x-32y)(x^2+1)=0$
$\Rightarrow 8x-32y=0$ (do $x^2+1>0$ với mọi $x$)
$\Leftrightarrow x=4y$
Khi đó:
$M=\frac{3.4y+2y}{3.4y-2y}=\frac{14y}{10y}=\frac{14}{10}=\frac{7}{5}$
https://hoc24.vn/hoi-dap/question/568186.html
link nè bn
2 câu đấy khác nhé bạn, đay là "-1" chứ không phải "+12"