làm giúp mình
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1/ Có 2 chi lưu: sông Chanh và sông Rút.
2/ Nhờ vào thuỷ triều của nước.
Mô tả: Quân ta dụ giặc đi vào sông Bạch Đằng khi thuỷ triều lên. Khi giặc thua trận và rút lui thì vừa lúc thuỷ triều xuống, bãi cọc nhô lên làm địch bị nhiều thiệt hại.

a. Đây là nước đá, nóng chảy ở 0oC.
c. Để...cần thời gian là 2 phút.
d. Sự nóng chảy bắt đầu từ phút thứ 2, kết thúc phút thứ 8
e. Thời gian nóng chảy là 6 phút.
f. Phút thứ 1 chất này tồn tại ở thể rắn, phút thứ 12 chất này tồn tại ở thể lỏng.
a, Chất này là nước. Chất này nóng chảy ở nhiệt độ \(0^0\).
b, Cần số thời gian để đưa chất tới nhiệt độ nóng chảy cần số thời gian là:
2-0=2(phút)
c,Sự nóng chảy bất đầu từ phút thứ 2
d,Thời gian diễn ra quá trình nóng chảy là:
8-2=6(phút)
e,Phút thứ 1 chất này tồn tại ở thể rắn. Phút thứ 12 chất này tồn tại ở thể lỏng và khí.

a:
\(AB=\dfrac{AC}{2}\)
\(AD=DC=\dfrac{CA}{2}\)
Do đó: AB=AD=DC
Xét ΔAHB vuông tại H và ΔCED vuông tại E có
AB=CD(cmt)
\(\widehat{HAB}=\widehat{ECD}\left(=90^0-\widehat{HBA}\right)\)
Do đó: ΔAHB=ΔCED
b: DE\(\perp\)BC
AH\(\perp\)BC
Do đó: DE//AH
Xét ΔCAH có
D là trung điểm của AC
DE//AH
Do đó: E là trung điểm của CH
=>EC=EH
Xét ΔDHC có
DE là đường cao
DE là đường trung tuyến
Do đó: ΔDHC cân tại D
c: ΔABD vuông tại A
mà AI là đường trung tuyến
nên \(AI=\dfrac{1}{2}BD\left(1\right)\)
ΔBED vuông tại E
mà EI là đường trung tuyến
nên \(EI=\dfrac{1}{2}BD\left(2\right)\)
Từ (1) và (2) suy ra AI=EI
ΔAHB=ΔCED
=>AH=CE
mà CE=EH
nên AH=EH
XétΔAHI và ΔEHI có
HA=HE
HI chung
AI=EI
Do đó: ΔAHI=ΔEHI
d: Xét ΔIDE có ID=IE
nên ΔIDE cân tại I
IK//BC
BC\(\perp\)DE
Do đó: IK\(\perp\)DE
ΔIDE cân tại I
mà IK là đường cao
nên IK là phân giác của góc DIE
=>\(\widehat{DIK}=\widehat{EIK}\)
Xét ΔIKD và ΔIKE có
IK chung
\(\widehat{KID}=\widehat{KIE}\)
ID=IE
Do đó: ΔIKD=ΔIKE
f: Xét tứ giác ADEB có
\(\widehat{DAB}+\widehat{DEB}=90^0+90^0=180^0\)
=>ADEB là tứ giác nội tiếp
=>\(\widehat{AED}=\widehat{ABD}=45^0\)

1.started smoking cigarettes a month ago
2. to walk at twenty minutes to school every morning
3.I haven't seen my uncle for two years
4.going to the movies tonight?
5.so stayed at home from school yesterday
6.me three hours to make...
7.gardening at the weekend
8.để nguyên vế sau
10.watching...
11.Minh ....
12.seen her since 2001
1. The last time he smoked was a month ago
2. it takes me twenty minutes to walk to school every morning.
3. I haven't seen my uncle for two years
4. Let's go to the movies tonight.
5. July had a high fever, so she stayed home from school yesterday.
6. I spent three hours making this pottery jug
7. My father enjoys gardening at the weekend
8. What about going swimming this afternoon?
9. My father is interested in playing board games.
10. He enjoys watching football very much.
11. Because Minh was sick, she could not go to school.
12. We haven't seen her since 2001


\(\dfrac{x}{-3}=\dfrac{y}{7}\Rightarrow\dfrac{x}{6}=\dfrac{y}{-14};\dfrac{y}{-2}=\dfrac{z}{5}\Rightarrow\dfrac{y}{-14}=\dfrac{z}{35}\\ \Rightarrow\dfrac{x}{6}=\dfrac{y}{-14}=\dfrac{z}{35}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{6}=\dfrac{y}{-14}=\dfrac{z}{35}=\dfrac{2x}{12}=\dfrac{4y}{-56}=\dfrac{5z}{175}=\dfrac{-2x-4y+5z}{-12+56+175}=\dfrac{146}{219}=\dfrac{2}{3}\\ \Rightarrow\left\{{}\begin{matrix}x=6\cdot\dfrac{2}{3}=4\\y=-14\cdot\dfrac{2}{3}=-\dfrac{28}{3}\\z=35\cdot\dfrac{2}{3}=\dfrac{70}{3}\end{matrix}\right.\)
x/-3=y/7;y/-2=z/5 và -2x-4y+5z=146
BCNN(7,2)=14
=>x/-3=y/7;y/-2=z/5
=>x/-3=y/7=>x/6=y/14(1)
=>y/-2=z/5=>y/-14=z/35(2)
từ(1) và (2) =>x/6=y/-14=z/35 và -2x-4y+5z=146
Sử dụng tính chất dãy tỉ số bằng nhau:
=>x/6=y/-14=z/35=>-2x-4y+5z/(-2).6-4.(-14)+5.35=146/219=2/3
=>x/6=2/3=>x=2.6/3=4
=>y/-14=2/3=>y=-14.2/3=-28/3
=>z/35=2/3=>z=35.2/3=70/3

 ! Giúp mình làm đề cương !
! Giúp mình làm đề cương !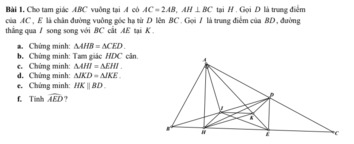





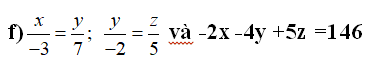 làm giúp mình với mình làm ơn đó ạ
làm giúp mình với mình làm ơn đó ạ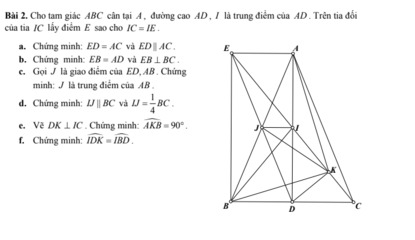
a) Vì \(\hept{\begin{cases}\left|x-y-2\right|\ge0∀x,y\\\left|y+3\right|\ge0∀y\end{cases}}\)\(\Rightarrow\left|x-y-2\right|+\left|y+3\right|≥0∀x,y\)
Dấu "=" xảy ra <=> \(\hept{\begin{cases}\left|x-y-2\right|=0\\\left|y+3\right|=0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x-y-2=0\\y+3=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x-y=2\\y=-3\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-1\\y=-3\end{cases}}\)
b) Vì \(\hept{\begin{cases}\left|x-3y\right|^{2007}\ge0∀x,y\\\left|y+4\right|^{2008}\ge0∀y\end{cases}}\)\(\Rightarrow\left|x-3y\right|^{2007}+\left|y+4\right|^{2008}≥0∀x,y\)
Dấu "=" xảy ra <=> \(\hept{\begin{cases}\left|x-3y\right|^{2007}=0\\\left|y+4\right|^{2008}=0\end{cases}}\Leftrightarrow\hept{\begin{cases}\left|x-3y\right|=0\\\left|y+4\right|=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x-3y=0\\y+4=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=3y\\y=-4\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-12\\y=-4\end{cases}}\)
c) Vì \(\hept{\begin{cases}\left(x+y\right)^{2006}\ge0∀x,y\\2007.\left|y-1\right|\ge0∀y\end{cases}}\)\(\Rightarrow\left(x+y\right)^{2006}+2007.\left|y-1\right|\ge0∀x,y\)
Dấu "=" xảy ra <=> \(\hept{\begin{cases}\left(x+y\right)^{2006}=0\\2007.\left|y-1\right|=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x+y=0\\\left|y-1\right|=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-y\\y-1=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=-y\\y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-1\\y=1\end{cases}}\)
d) Vì \(\hept{\begin{cases}\left|x-y-5\right|\ge0∀x,y\\2007.\left(y-3\right)^{2008}\ge0∀y\end{cases}}\)\(\Rightarrow\left|x-y-5\right|+2007.\left(y-3\right)^{2008}\ge0\ge0∀x,y\)
Dấu "=" xảy ra <=> \(\hept{\begin{cases}\left|x-y-5\right|=0\\2007.\left(y-3\right)^{2008}=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x-y-5=0\\\left(y-3\right)^{2008}=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x-y=5\\y-3=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x-y=5\\y=3\end{cases}}\Leftrightarrow\hept{\begin{cases}x=8\\y=3\end{cases}}\)