Chứng minh biểu thức sau không phụ thuộc vào giá trị của biến x
A=(xn+1)(xn-2)-xn-3(xn+3-x3)+2013
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
K
2
Những câu hỏi liên quan
5 tháng 7 2019
Câu hỏi của Thi Bùi - Toán lớp 7 - Học toán với OnlineMath
Bạn tham khảo link trên nhé!
MN
23 tháng 4 2019
Bài 1 :
8x - 0,4 = 7,8*x + 402
8x - 7,8*x = 402 + 0,4
0,2*x = 402,04
x= 402,04 : 0,2
x = 2012
MN
23 tháng 4 2019
Bài 2
Theo bài ra , số học sinh lớp 6A bằng 1/2 tổng số học sinh hai lớp 6B và 6C
=> Số học sinh lớp 6A bằng 1/3 số học sinh của cả 3 lớp
Số học sinh lớp 6A là :
120 x 1/3 = 40 học sinh
Tổng số học sinh lớp 6B và 6C là :
120 - 40 = 80 học sinh
Số học sinh lớp 6B là :
( 80 - 6 ) : 2 = 37 học sinh
Số học sinh lớp 6C là :
37 + 6 = 43 học sinh
LP
1
19 tháng 9 2021
\(A=\left(x^2-2\right)\left(x^2+x+1\right)-x\left(x^3+x^2-3x-2\right)=x^4+x^3-x^2-2x^2-2x+2-x^4-x^3+3x^2+2x=2\left(đpcm\right)\)
AH
Akai Haruma
Giáo viên
20 tháng 9 2021
Lời giải:
$A=(x^4+x^3-x^2-2x^2-2x+2)-(x^4+x^3-3x^2-2x)$
$=(x^4+x^3-3x^2-2x+2)-(x^4+x^3-3x^2-2x)$
$=(x^4+x^3-3x^2-2x)+2-(x^4+x^3-3x^2-2x)$
$=2$ khong phụ thuộc vào giá trị của biến $x$ (đpcm)
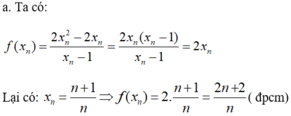
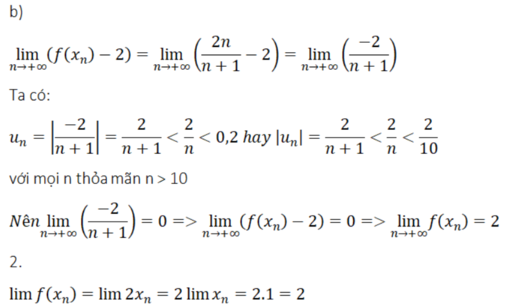
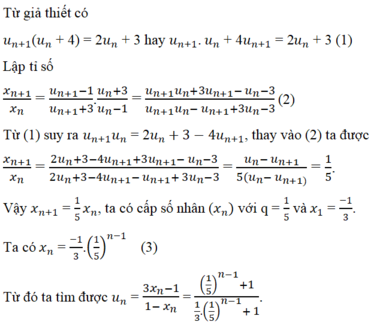
nhân ra ko đc à em
nhân ra sau là tính đc mà
hok tốt
\(A=\left(x^n+1\right)\left(x^n-2\right)-x^{n-3}\left(x^{n+3}-x^3\right)+2013\)
\(A=x^n\cdot x^n-x^n\cdot2+x^n-2-x^{n-3}\cdot x^{n+3}+x^{n-3}\cdot x^3+20\)
\(A=x^{2n}-2x^n+x^n-x^{n-3+n+3}+x^{n-3+3}+20-2\)
\(A=x^{2n}-2x^n+x^n-x^{2n}+x^n+18\)
\(A=\left(x^{2n}-x^{2n}\right)-\left(2x^n-x^n-x^n\right)+18\)
\(A=0-0+18\)
\(A=18\)
Với mọi x thì A luôn bằng 18
Vậy giá trị của A không phụ thuộc vào biến x ( đpcm )