y2 - 10x = 48
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
27 tháng 9 2018
Xét x = 0 thì: 10 0 + 48 = y 2 ⇔ y 2 = 49 = 7 2 => y = 7
Xét với x ≠ 0 thì 10 x có chữ số tận cùng là 0, Do đó 10 x + 48 có tận cùng là 8
Mà y 2 là số chính phương nên không thể có tận cùng là 8
Vậy x = 0, y = 7
PT
1
2V
1
12 tháng 10 2021
\(x^2-25=\left(x-5\right)\left(x+5\right)\\ x^2+10x+25=\left(x+5\right)^2\\ x^2-6x+xy-6y=x\left(x-6\right)+y\left(x-6\right)=\left(x+y\right)\left(x-6\right)\\ x^2-2x-y^2+1=\left(x-1\right)^2-y^2=\left(x-y-1\right)\left(x+y-1\right)\)
VD
3
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
22 tháng 8 2023
\(=\left(x-y\right)\left(x+y\right)-10\left(x+y\right)=\)
\(=\left(x+y\right)\left(x-y-10\right)\)
22 tháng 8 2023
= (x - y). (x + y) - 10 ( x - y)
= [( x + y) - 10)] . ( x - y)
KB
1
AH
Akai Haruma
Giáo viên
5 tháng 9 2020
Lời giải:
Ta thấy:
$10x\equiv 0\pmod 5$
$288\equiv 3\pmod 5$
$\Rightarrow y^2\equiv 3\pmod 5$ (vô lý)
Do ta biết rằng một số chính phương khi chia cho $5$ chỉ có thể có dư là $0,1,4$.
Như vậy, không tồn tại số tự nhiên $x,y$ thỏa mãn điều kiện đề bài.
NH
0
NH
2
11 tháng 8 2021
a) Ta có: \(M=x^2-2xy+y^2-10x+10y\)
\(=\left(x-y\right)^2-10\left(x-y\right)\)
\(=9^2-10\cdot9=-9\)
CM
17 tháng 6 2017
Ta có hệ số a= 5; b= 0 và c= -11 nên bán kính là R= a 2 + b 2 - c = 6
Chọn A.
CM
9 tháng 5 2017
Ta có: đường tròn: x2+ y2- 10x + 1= 0 => (x- 5)2 + y2= 24 có tâm I(5;0) .Khoảng cách từ I đến Oy là d ( I ; O y ) = 5
Chọn D.
K
1
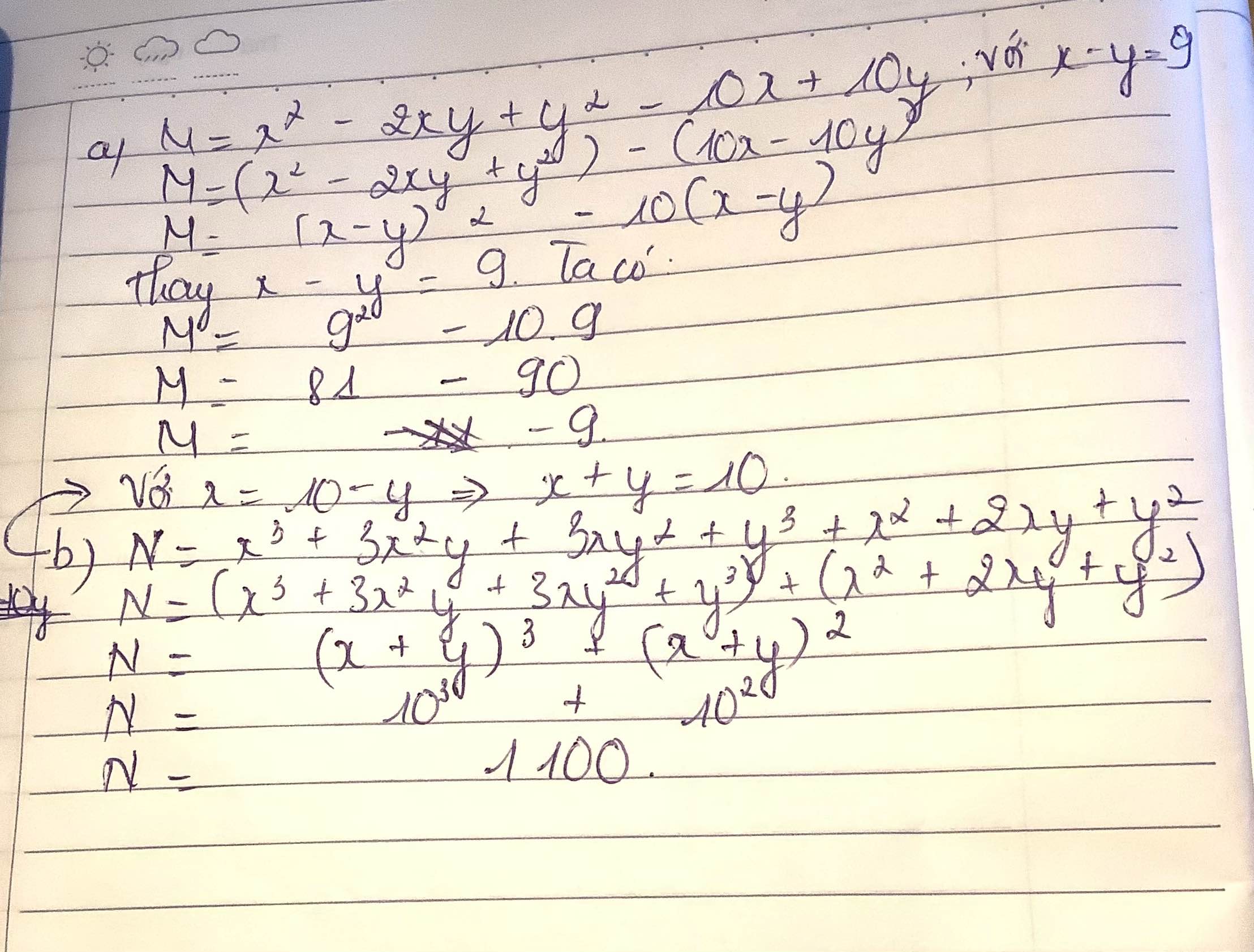
\(y^2=48+10^x\)
Với x=0 thì y=7
x>0 thì 10x có dạng 100.........000 và có tận cùng là 0
nên 10x +48 sẽ có dạng 100.........048 và có tận cùng là 8
Ta có: y2 là số chính phương nên 10x +48 cũng phải là số chính phương
mà ko có số chính phương nào có tận cùng là 8 nên không tồn tại x,y thỏa mãn x>0 ,10x +48 =y2
Vậy x=0 ,y=7