Gọi \(\alpha\) là góc tạo bởi đường thẳng \(y=-12x+3\) và trục Ox.
Khi đó \(tan\left(180-\alpha\right)=\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 11 2015
Gọi a1 là góc kề bù với a
Ta có tana1 =12 => a1 = 85
=> a +a1 =180 => 180 -a =a1 =85 độ
KQ: 85 độ 14phut10 giay...
KS
0
HQ
Hà Quang Minh
Giáo viên
12 tháng 9 2023
b)
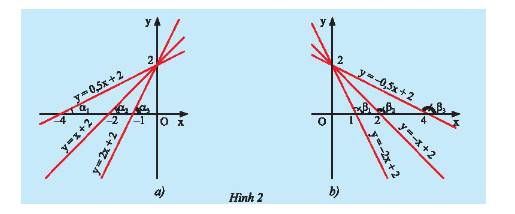
- Ở hình 2a là đồ thị của 3 hàm số \(y = 0,5x + 2;y = x + 2;y = 2x + 2\).
Ta có: \({a_1} = 0,5;{a_2} = 1;{a_3} = 2\) nên \({a_1} < {a_2} < {a_3}\).
Ta có: \({\alpha _1} < {\alpha _2}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
\({\alpha _2} < {\alpha _3}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
Do đó, \({\alpha _1} < {\alpha _2} < {\alpha _3}\).
- Ở hình 2b là đồ thị của 3 hàm số \(y = - 2x + 2;y = - x + 2;y = - 0,5x + 2\).
Ta có: \({a_1} = - 2;{a_2} = - 1;{a_3} = - 0,5\) nên \({a_1} < {a_2} < {a_3}\).
Ta có: \({\beta _1} < {\beta _2}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
\({\beta _2} < {\beta _3}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
Do đó, \({\beta _1} < {\beta _2} < {\beta _3}\).
PT
1
6 tháng 1 2017
Thì bằng \(-2016\) chứ còn bằng bao nhiêu nữa? Đây là tính chất của hệ số góc mà.
AH
Akai Haruma
Giáo viên
26 tháng 7 2021
Lời giải:
Gọi $O$ là tâm đáy thì $SO\perp (ABCD)$
Ta thấy:
$BO\perp AC, BO\perp SO\Rightarrow BO\perp (AC, SO)$
Hay $BO\perp (SAC)(*)$
Gọi $T$ là trung điểm $AB$, $OH\perp ST$.
$OT\perp AB$
$SO\perp AB$
$\Rightarrow (SOT)\perp AB$
$\Rightarrow OH\perp AB$
Mà $OH\perp ST$
$\Rightarrow OH\perp (AB, ST)$ hay $OH\perp (SAB)(**)$
Từ $(*); (**)\Rightarrow \cos a=\cos \widehat{HOB}$
Trong đó:
$BO=\frac{2\sqrt{2}}{2}=\sqrt{2}$
$SO=\sqrt{SB^2-BO^2}=\sqrt{(2\sqrt{2})^2-(\sqrt{2})^2}=\sqrt{6}$
$ST=\sqrt{SO^2+OT^2}=\sqrt{6+1}=\sqrt{7}$
$OH=\frac{SO.OT}{ST}=\frac{\sqrt{6}.1}{\sqrt{7}}=\sqrt{\frac{6}{7}}$
Vì $OH\perp (SAB)$ nên tam giác $BHO$ vuông tại $H$. Do đó:
$\cos a=\cos \widehat{HOB}=\frac{HO}{OB}=\frac{\sqrt{6}}{\sqrt{7}.\sqrt{2}}=\frac{\sqrt{3}}{\sqrt{7}}$