Tìm các giá trị x và y thỏa mãn biết : x2 -y2 =5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 10 2017
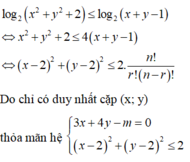
nên đường thẳng 3x + 4y - m = 0 là tiếp tuyến của đường tròn (x – 2)2 + (y – 2)2 = 2.
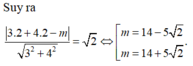
Chọn C.
CM
1 tháng 11 2017
Từ giả thiết bài toán suy ra
y ≥ 0 x 2 2 ≤ - 2 x 2 + 3 x ⇔ y ≥ 0 5 x 2 - 6 x ≤ 0 ⇔ y ≥ 0 0 ≤ x ≤ 6 5
Ta có
x 2 + y 2 ≤ x 2 + - 2 x 2 + 3 x 2 = 4 x 4 - 12 x 3 + 10 x 2
Ta có f ' x = 4 x x - 1 x - 5
f ' x = 0 x = 0 x = 1 x = 5 So điều kiện, chọn x = 0 ; x = 1 ; f(0); f(1) = 2; f 6 5 = 1224 625
Vậy m a x P = 2
Đáp án D
CM
14 tháng 4 2019
Vì x và y là hai đại lượng tỉ lệ nghịch
⇒ x1y1 = x2y2 hay 2y1 = 5y2
CM
1 tháng 7 2019
Do x, y là hai đại lượng tỉ lệ nghịch nên ta có:
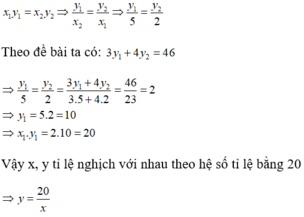
Chọn đáp án C
24 tháng 5 2021
\(x^2+y^2+xy=3\)
Có \(x^2+y^2\ge2xy\) \(\Rightarrow3=x^2+y^2+xy\ge2xy+xy\) \(\Leftrightarrow xy\le1\)
\(x^2+y^2\ge-2xy\) \(\Rightarrow3=x^2+y^2+xy\ge-2xy+xy\) \(\Leftrightarrow-3\le xy\)
Đặt A= \(x^2+y^2-xy=\left(3-xy\right)-xy=3-2xy\)
mà \(-3\le xy\le1\) \(\Rightarrow9\ge3-2xy\ge1\)
=> minA=1 <=> \(\left\{{}\begin{matrix}xy=1\\x=y\end{matrix}\right.\) <=>x=y=1
maxA=9 <=>\(\left\{{}\begin{matrix}xy=-3\\x=-y\end{matrix}\right.\) <=>\(\left(x;y\right)=\left(\sqrt{3};-\sqrt{3}\right);\left(-\sqrt{3};\sqrt{3}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 5 2021
Đặt \(P=x^2+y^2-xy\)
\(\Rightarrow\dfrac{P}{3}=\dfrac{x^2+y^2-xy}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}\)
\(\dfrac{P}{3}=\dfrac{3x^2+3y^2-3xy}{3\left(x^2+y^2+xy\right)}=\dfrac{x^2+y^2+xy+2\left(x^2+y^2-2xy\right)}{3\left(x^2+y^2+xy\right)}\)
\(\dfrac{P}{3}=\dfrac{1}{3}+\dfrac{2\left(x-y\right)^2}{3\left(x^2+y^2+xy\right)}\ge\dfrac{1}{3}\Rightarrow P\ge1\)
\(P_{min}=1\) khi \(x=y=1\)
\(\dfrac{P}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}=\dfrac{3\left(x^2+y^2+xy\right)-2\left(x^2+y^2+2xy\right)}{x^2+y^2+xy}=3-\dfrac{2\left(x+y\right)^2}{x^2+y^2+xy}\le3\)
\(\Rightarrow P\le9\)
\(P_{max}=9\) khi \(\left(x;y\right)=\left(\sqrt{3};-\sqrt{3}\right);\left(-\sqrt{3};\sqrt{3}\right)\)
xem lại đề
Đề ko sai