Cho tứ giác lồi ABCD. GỌI M là một điểm nằm bên trong tứ giác và N là một điểm nằm bên ngoài tứ giác. biết các tứ giác ABMD, BMCN LÀ hình bình hành,. CHỨNG MINH GÓC NAB bằng góc MDC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: Xét tứ giác EBFD có
ED//BF
ED=BF
Do đó: EBFD là hình bình hành

Giả sử tứ giác ABCD định hướng âm. Gọi \(f\) là phép quay vec tơ theo góc \(\frac{\pi}{3}\) ta có
\(\overrightarrow{EG}=\overrightarrow{AG}-\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{BG}-\overrightarrow{AE}\)
suy ra \(f\left(\overrightarrow{EG}\right)=f\left(\overrightarrow{AB}\right)+f\left(\overrightarrow{BG}\right)-f\left(\overrightarrow{AE}\right)\)
\(=\overrightarrow{AE}+\overrightarrow{BC}-\overrightarrow{BE}\)
\(=\overrightarrow{AC}\)
Tương tự ta cũng chứng minh được \(f\left(\overrightarrow{HF}\right)=\overrightarrow{AC}\)
Từ đó suy ra \(\overrightarrow{EG}=\overrightarrow{HF}\)
Do đó tứ giác EGFH là hình bình hành

a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó:AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
từ (1) và (2) suy ra OA\(\perp\)BC(3)
b: Xét (O) có
ΔDBC nội tiếp
DC là đường kính
Do đó: ΔDBC vuông tại B
=>BC\(\perp\)BD(4)
Từ (3) và (4) suy ra BD//OA

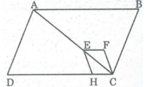
Hình ABCFE không phải là tứ giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh CF.