Mong mọi người giúp rút gọn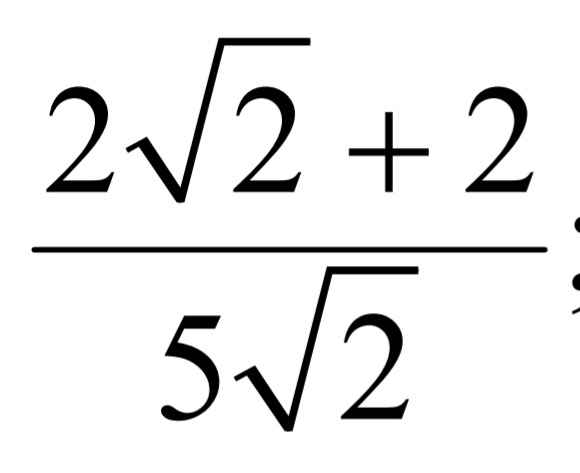
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A = 1 + 3 + 32 + 33 + ... + 360
3A = 3 + 32 + 33 + 34 + ... + 361
3A - A = (3 + 32 + 33 + 34 + ... + 361) - (1 + 3 + 32 + 33 + ... + 360)
2A = 361 - 1
\(A=\frac{3^{61}-1}{2}\)
3A=3+32+33+34+...+360+361
3A - A=(3+32+33+34+...+360+361) - (1+3+32+33+....+360)
2A=361-1
A =\(\frac{3^{61}-1}{2}\)

Đặt \(A=2^{17}-2^{16}-2^{15}-...-2^2-2-1\) ta có :
\(A=2^{17}-\left(2^{16}+2^{15}+...+2+1\right)\)
Đặt \(B=2^{16}+2^{15}+...+2+1\) ta có :
\(2B=2^{17}+2^{16}+...+2^2+2\)
\(2B-B=\left(2^{17}+2^{16}+...+2^2+2\right)-\left(2^{16}+2^{15}+...+2+1\right)\)
\(B=2^{17}-1\)
\(\Rightarrow\)\(A=2^{17}-B=2^{17}-\left(2^{17}-1\right)=2^{17}-2^{17}+1=1\)
Vậy \(A=1\)
Chúc bạn iu họk tốt :3

\(\frac{-1997\cdot1996+1}{-1995\cdot\left(-1997\right)+1996}\)
\(=\frac{-1997\cdot\left(1995+1\right)+1}{1995\cdot1997+1996}\)
\(=\frac{-1997\cdot1995+\left(-1997\right)+1}{1995\cdot1997+1996}\)
\(=\frac{-1997\cdot1995+\left(-1996\right)}{1995\cdot1997+1996}\)
\(=-1\)
\(\frac{-1997.1996+1}{-1995.\left(-1997\right)+1996}\)
\(=\frac{-1997.1996+1}{1995.1997+1996}\)
\(=\frac{-1997.\left(1995+1\right)+1}{1995.1997+1996}\)
\(=\frac{-1997.1995+-1997+1}{1995.1997+1996}\)
\(=\frac{1995.-1997+-1996}{1995.1997+1996}\)
\(=\frac{-\left(1995.1997+1996\right)}{1995.1997+1996}\)
\(=-1\)

Phân số sau khi rút gọn là :
\(\frac{2}{7}\);\(\frac{5}{7}\);\(\frac{3}{5}\);\(\frac{3}{7}\).
Sắp xếp theo thứ tự tăng dần là :
\(\frac{2}{7}\);\(\frac{3}{7}\);\(\frac{3}{5}\);\(\frac{5}{7}\).
Kik mik nha ! Hok tốt !

\(\sqrt{117,5^2-26,5^2}-1440=-202475\)
\(\sqrt{146,5^2-109,5^2+27,256=}-11816494\)

\(\dfrac{6}{\sqrt{2}-\sqrt{3}+3}=\dfrac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{8-2\sqrt{6}}=\dfrac{3\left(\sqrt{2}-\sqrt{3}-3\right)\left(4+\sqrt{3}\right)}{13}\)

\(A=\left(\dfrac{\sqrt{x}-2}{x-1}-\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right)\cdot\dfrac{\left(x-1\right)^2}{2}\)
\(=\dfrac{x-\sqrt{x}-2-\sqrt{x}-\sqrt{x}+2}{\left(\sqrt{x}-1\right)^2\cdot\left(\sqrt{x}+1\right)}\cdot\dfrac{\left(x-1\right)^2}{2}\)
\(=-\sqrt{x}\cdot\left(\sqrt{x}+1\right)\)

\(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{2\sqrt{x}}{x-1}-\dfrac{1}{\sqrt{x}+1}\left(đk:x\ne1,x\ge0\right)\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)-2\sqrt{x}-\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x+\sqrt{x}-2\sqrt{x}-\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
ĐKXĐ: \(x\ne1,x\ge0\)
\(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{2\sqrt{x}}{x-1}-\dfrac{1}{\sqrt{x}+1}=\)\(\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{x-1}-\dfrac{2\sqrt{x}}{x-1}-\dfrac{\sqrt{x}-1}{x-1}=\)\(\dfrac{x+\sqrt{x}-2\sqrt{x}-\sqrt{x}+1}{x-1}=\)\(\dfrac{x-2\sqrt{x}+1}{x-1}=\)\(\dfrac{(\sqrt{x}-1)^2}{x-1}=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
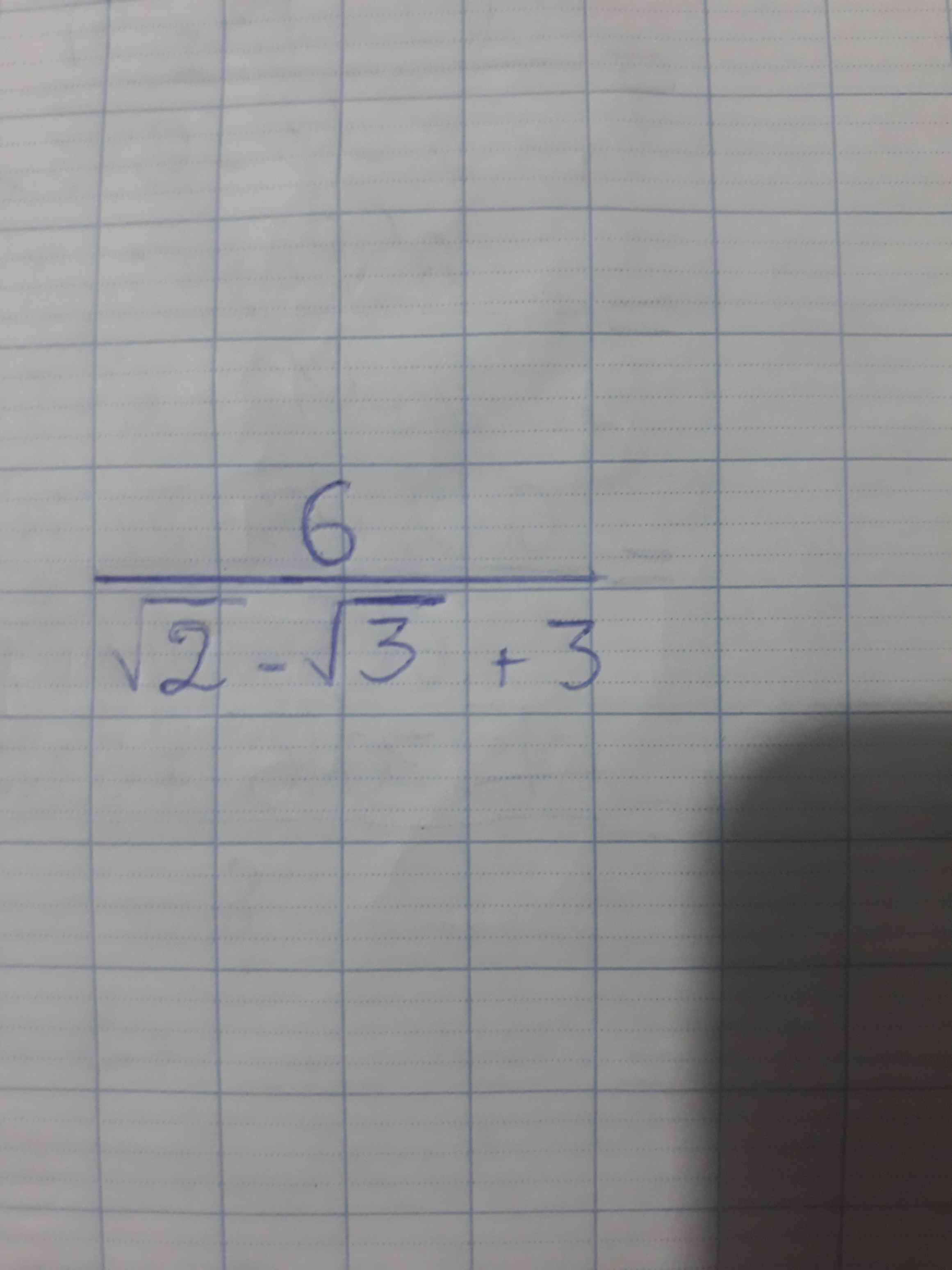
\(=\dfrac{\sqrt{2}\left(2+\sqrt{2}\right)}{5\sqrt{2}}=\dfrac{2+\sqrt{2}}{5}\)
\(\dfrac{2\sqrt{2}+2}{5\sqrt{2}}=\dfrac{\sqrt{2}\left(2+\sqrt{2}\right)}{5\sqrt{2}}=\dfrac{2+\sqrt{2}}{5}\)