Một người đi xe máy theo kiểu "nhảy bậc" ở cuối mỗi phút : v1=40 km/h , v2= 60 km/h , v3=80 km/h , v4=20 km/h. Tính vttb của xe?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tóm tắt:
GT:SAB=10km
SBC=5km
V1=50km/h
V2=30km/h
V3=20km/h
____________
KL: t=? ; SBB'=?
Bài Làm:
Gọi: + t là thời gian đi của 3 xe.
+ A′, B′, C′ lần lượt là các điểm để thỏa mãn điều kiện đề ra của xe 1, xe 2, xe 3.

Ta có: SAB' − SAA' = SAC − SAB′ ⇒ 2SAB′ = SAA + SAC′ ⇒ 2(SAB+SBB′) = SAA′ + 15 + SCC′
⇒ 2(10+V2.t) =V1.t + 15 + V3.t ⇒ 20 + 2.30t = 50t + 15 + 20t ⇒ 20 + 60t = 70t + 15
⇒70t − 60t = 20−15 ⇒10t=5⇒t=0,5(h)
Vậy: Khi đó xe 2 đi được quãng đường là: SBB′ = V2.t = 30.0,5 = 15(km)

vận tốc trung bình của người đó trên cả quãng đường là:
\(v_{tb}=\dfrac{\dfrac{t}{2}\left(v_1+v_{tb2}\right)}{t}\Rightarrow30=\dfrac{1}{2}\left(40+v_{tb2}\right)\Rightarrow v_{tb2}=20\left(\dfrac{km}{h}\right)\)
vận tốc trung bình của người đó trên phần đường còn lại là:
\(v_{tb2}=\dfrac{s_2}{\dfrac{s_2}{2}\left(\dfrac{1}{v_2}+\dfrac{1}{v_3}\right)}\Rightarrow20=\dfrac{1}{\dfrac{1}{2}\left(\dfrac{1}{30}+\dfrac{1}{v_3}\right)}\Rightarrow v_3=15\left(\dfrac{km}{h}\right)\)
vậy ...

Sau 1h xe đi từ A --> B đi được số km là
\(s_1=v_1t=30.1=30\left(km\right)\)
Sau 1h xe đi từ B --> A đi được số km là
\(s_2=v_2t=40.1=40\left(km\right)\)
Khoảng cách 2 xe là
\(=\left(60-30\right)+40=70\left(km\right)\)
1h30p = 1,5 h
Gọi t là tgian sau 1,5h đến lúc 2 xe gặp nhau
Xe A --> B đi được số km là
\(s_3=1,5.30+50t\)
Xe B --> A đi được
\(s_4=1,5.40+40t\)
VD gặp nhau ở E
Vậy nên ta có vận tốc 2 xe gặp nhau là
\(s_3=s_4+AB\\ \Rightarrow1,5.30+50t=1,5.40+40t+60\\ \Rightarrow t=7,5\left(h\right)\)
Sau giờ 2 xe gặp nhau là
\(7,5+1,5=9\left(h\right)\)
Vị trí gặp cách A là
\(=1,5.30+50.7,5=420\left(km\right)\)

Sau khi đi được 15p xe máy đến C cách A 10km gặp xe ô tô. Ô tô đến A vs thời gian t=10/60=1/6(h) Ô tô nghỉ 30 phút tổng thời gian là 1/6+1/2=2/3(h)
Đặt D là điểm cách B 25km nơi 2 xe gặp nhau. Đặt X là độ dài đoạn CD. Thời gian xe máy đi từ C đến D từ khi gặp xe ô tô là X/40. Thời gian xe ô tô đi từ khi gặp xe máy lần 1 đến khi gặp xe máy lần 2 là: 2/3+(X+10)/60. Ta có 2/3+(X+10)/60=X/40
Giải phương trình trên ta được X=100. Trường hợp D nằm giữa C và B thì độ dài đoạn AB bằng 135km Trường hợp B nằm giữa C và D thì độ dài đoạn AB bằng 85km. Vì xe máy ko đi quá B nên loại trường hợp B nằm giữa C và D vậy dộ dài đoạn AB là 135km
# mui #

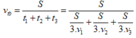

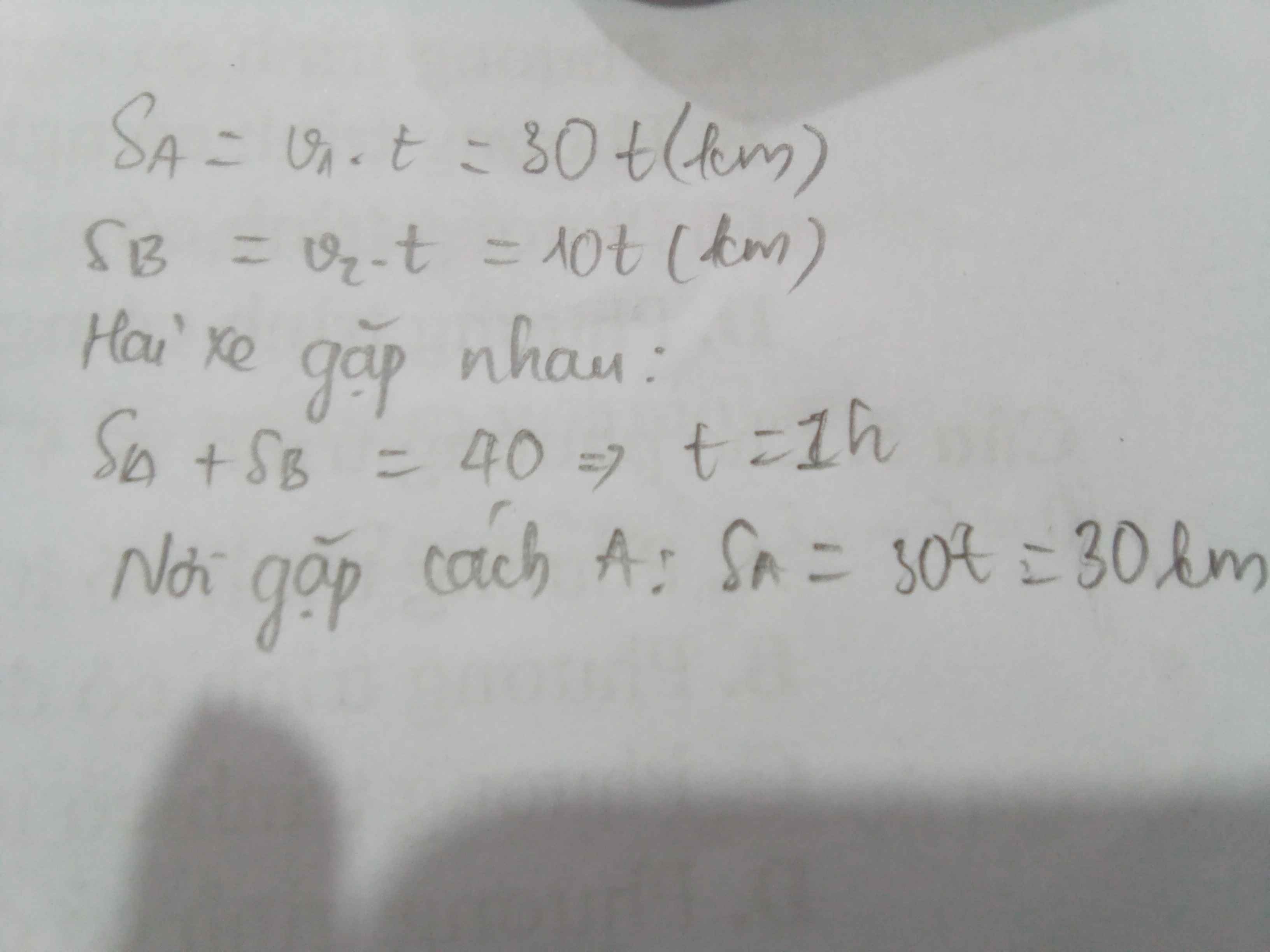
vtb=50km/h