nhờ mn giúp em với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tham khao
Bài 1: Cho nửa đường tròn (O) đường kính AB= 2R, dây cung AC. Gọi M là điểm chính giữa cung AC. Một đường thẳng kẻ từ điểm C song song với BM và cắt AM ở K , cắt OM ở D. OD cắt AC tại H.
1. Chứng minh CKMH là tứ giác nội tiếp.
2. CMR : CD = MB ; DM = CB.
3. Xác điểm C trên nửa đường tròn (O) để AD chính là tiếp tuyến của nửa đường tròn.
Bài 2: Cho ABC có 3 góc nhọn. Đường tròn có đường kính BC cắt hai cạnh AB, AC lần lượt tại các điểm E và F ; BF cắt EC tại H. Tia AH BC tại điểm N.
a) CMR: tứ giác HFCN là tứ giác nội tiếp.
b) CMR: FB là tia phân giác của góc EFN.
c) Nếu AH = BC. Hãy tìm số đo góc BAC trong ΔABC.

Bài 3: Cho nửa đường tròn tâm O và nó có đường kính AB. Từ một điểm M nằm trên tiếp tuyến Ax của nửa đường tròn, ta vẽ tiếp tuyến thứ hai tên gọi là MC (trong đó C là tiếp điểm). Từ C hạ CH vuông góc với AB, MB cắt (O) tại điểm Q và cắt CH tại điểm N. Gọi g I = MO ∩ AC. CMR:
a) Tứ giác AMQI là tứ giác nội tiếp.
b) Góc AQI = góc ACO
c) CN = NH.
(Trích đề thi tuyển sinh vào lớp 10 năm học 2009-2010 của sở GD&ĐT Tỉnh Bắc Ninh)

Bài 4: Cho đường tròn (O) có đường kính là AB. Trên AB lấy một điểm D nằm ngoài đoạn thẳng AB và kẻ DC là tiếp tuyến của đường tròn (O) (với C là tiếp điểm). Gọi E là hình chiếu hạ từ A xuống đường thẳng CD và F là hình chiếu hạ từ D xuống AC.
Chứng minh:
a) Tứ giác EFDA là tứ giác nội tiếp.
b) AF là tia phân giác của góc EAD.
c) Tam giác EFA và BDC là hai tam giác đồng dạng.
d) Hai tam giác ACD và ABF có cùng diện tích với nhau.
(Trích đề thi tốt nghiệp và xét tuyển vào lớp 10- năm học 2000- 2001)

Bài 5: Cho tam giác ABC (BAC < 45o) là tam giác nội tiếp trong nửa đường tròn tâm O có đường kính AB. Vẽ tiếp tuyến của đường tròn (O) tại C và gọi H là hình chiếu kẻ từ A đến tiếp tuyến . Đường thẳng AH cắt đường tròn (O) tại M (M ≠ A). Đường thẳng kẻ từ M vuông góc với AC cắt AC tại K và AB tại P.
a) CMR tứ giác MKCH là một tứ giác nội tiếp.
b) CMR: MAP là tam giác cân.
c) Hãy chỉ ra điều kiện của ΔABC để M, K, O cùng nằm trên một đường thẳng.


II. Phần tự luận
Câu 1: Động năng của một vật phụu thuộc vào khối lượng và vận tốc
Ví dụ về vật vừa có động năng vừa có thế năng: một chiếc lá đang rơi từ trên cây xuống
Câu 2: Vì nếu cho đá vào trước thì đường và chanh sẽ chậm hòa tan vàotrong nước do nhiệt độ càn cao thì các hạt nguyên tử phân tử chuyển động càng nhanh nên cần hòa tan đường và chanh vào trước để được hòa tan vào trong nước hơn rồi mới nên cho đá vào
II. Phần tự luận:
Câu 3:
Công thực hiện được:
\(A=F.s=180.8=1440J\)
Công suất của người kéo:
\(\text{℘}=\dfrac{A}{t}=\dfrac{1440}{30}==48W\)
Câu 4:
Đổi: \(12km/h=43,2m/s\)
Công suất của ngựa:
\(\text{℘}=\dfrac{A}{t}=\dfrac{F.s}{t}=F.\dfrac{s}{t}=F.\upsilon=320.43,2=13824W\)

Dưới đây là một kịch bản gọi lửa Lạc Long Quân và Âu Cơ mà bạn có thể sử dụng:
Kịch bản: Gọi lửa Lạc Long Quân và Âu Cơ
Nhân vật:
Người dẫn chương trìnhDiễn viên 1: Lạc Long QuânDiễn viên 2: Âu CơBối cảnh: Sân khấu trang trọng, có bàn thờ ở giữa.
Người dẫn chương trình: Xin chào mừng quý vị đến với buổi biểu diễn gọi lửa Lạc Long Quân và Âu Cơ. Chúng ta sẽ cùng chứng kiến một phần trong huyền thoại về nguồn gốc của dân tộc Việt Nam. Hãy chào đón Lạc Long Quân và Âu Cơ!
(Đèn sân khấu tắt, sau đó sáng lên và hiện ra Lạc Long Quân và Âu Cơ đứng sát bàn thờ)
Người dẫn chương trình: Lạc Long Quân và Âu Cơ là hai vị thần thánh trong truyền thuyết Việt Nam. Họ là cha mẹ của dân tộc ta, người đặt nền móng cho sự phát triển và thịnh vượng của đất nước.
Lạc Long Quân (nghiêng đầu): Xin chào mọi người. Tôi là Lạc Long Quân, người đã đến từ biển cả xa xôi.
Âu Cơ (nghiêng đầu): Xin chào mọi người. Tôi là Âu Cơ, người đã đến từ trời cao.
Người dẫn chương trình: Hai vị thần thánh này đã gặp nhau và đến với nhau, tạo nên tình yêu và hôn nhân đầu tiên trong lịch sử con người.
Lạc Long Quân: Từ tình yêu chúng ta, đã sinh ra 100 con, được gọi là Hùng Vương, những người đã xây dựng và lãnh đạo nước Việt.
Âu Cơ: Tình yêu và sự đoàn kết của chúng ta đã truyền cảm hứng cho con cháu chúng ta, để họ xây dựng đất nước hùng mạnh và văn minh.
Người dẫn chương trình: Hôm nay, chúng ta sẽ cùng chứng kiến sự kết hợp giữa lửa của Lạc Long Quân và Âu Cơ, biểu trưng cho sự hòa hợp và thịnh vượng.
(Lạc Long Quân và Âu Cơ tiến lại gần bàn thờ. Họ cùng nhấc tay lên và tạo thành một vòng tròn. Đèn sân khấu sáng rực, tượng trưng cho lửa bén trong lòng đất nước)
Người dẫn chương trình: Hãy cùng nhìn thấy sự hòa quyện của hai thần thánh này, tạo nên nguồn lửa đại diện cho sự phát triển và thịnh vượng của dân tộc Việt Nam.
(Cả khán phòng vỗ tay tán thưởng)
Người dẫn chương trình: Cảm ơn Lạc Long Quân và Âu Cơ đã đến với chúng ta hôm nay. Hãy cùng nhau trân trọng và gìn giữ tình yêu và đoàn kết để xây dựng một đất nước ngày càng văn minh và phát triển.
Lưu ý: Đây chỉ là một mô phỏng ngắn về cách gọi lửa Lạc Long Quân và Âu Cơ trong một buổi biểu diễn. Bạn có thể tùy chỉnh kịch bản này hoặc thêm các yếu tố khác để phù hợp với nhu cầu của bạn.



a: Xét (O) có
ΔABN nội tiếp
AB là đường kính
Do đó: ΔABN vuông tại N
=>AN\(\perp\)NB tại N
=>BN\(\perp\)AM tại N
Xét (O) có
ΔAHB nội tiếp
AB là đường kính
Do đó: ΔAHB vuông tại H
=>AH\(\perp\)HB tại H
=>BH\(\perp\)AD tại H
Xét ΔBAM vuông tại B có BN là đường cao
nên \(AN\cdot AM=AB^2\left(1\right)\)
Xét ΔABD vuông tại B có BH là đường cao
nên \(AH\cdot AD=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(AN\cdot AM=AH\cdot AD\)
c: ta có: ΔOAN cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)AN
Xét ΔIAO vuông tại I và ΔNBM vuông tại N có
\(\widehat{IAO}=\widehat{NBM}\left(=90^0-\widehat{AMB}\right)\)
Do đó: ΔIAO~ΔNBM
Xét tứ giác OIMB có
\(\widehat{OBM}+\widehat{OIM}=90^0+90^0=180^0\)
nên OIMB là tứ giác nội tiếp
=>\(\widehat{MOB}=\widehat{MIB}\)
Xét ΔOBM vuông tại B và ΔINB vuông tại N có
\(\widehat{BOM}=\widehat{NIB}\left(cmt\right)\)
Do đó: ΔOBM~ΔINB


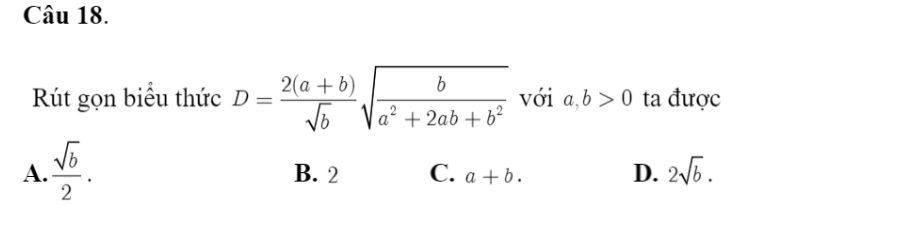
\(D=\dfrac{2\left(a+b\right)}{\sqrt{b}}.\dfrac{\sqrt{b}}{\sqrt{\left(a+b\right)^2}}=\dfrac{2\left(a+b\right).\sqrt{b}}{\sqrt{b}\left(a+b\right)}=2\)
=> Chọn B


a: \(3x-12-4\sqrt{x}+8=6\sqrt{2x+1}-18\)
=>\(\left(x-4\right)\cdot3-4\left(\sqrt{x}-2\right)=6\left(\sqrt{2x+1}-3\right)\)
=>\(3\left(x-4\right)-\dfrac{4\left(x-4\right)}{\sqrt{x}+2}-6\cdot\dfrac{2x+1-9}{\sqrt{2x+1}+3}=0\)
=>\(\left(x-4\right)\left(3-\dfrac{4}{\sqrt{x}+2}-\dfrac{12}{\sqrt{2x+1}+3}\right)=0\)
=>x-4=0
=>x=4
b: \(\Leftrightarrow\sqrt{x^2+x-1}-1+\sqrt{x-x^2+1}-1=x^2-x\)
=>\(\dfrac{x^2+x-1-1}{\sqrt{x^2+x-1}+1}+\dfrac{x-x^2+1-1}{\sqrt{x-x^2+1}+1}=x\left(x-1\right)\)
=>\(\dfrac{\left(x+2\right)\left(x-1\right)}{\sqrt{x^2+x-1}+1}-\dfrac{x\left(x-1\right)}{\sqrt{x-x^2+1}+1}-x\left(x-1\right)=0\)
=>\(\left(x-1\right)\left(\dfrac{x+2}{\sqrt{x^2+x-1}+1}-\dfrac{x}{\sqrt{x-x^2+1}+1}-x\right)=0\)
=>x-1=0
=>x=1
c: \(\Leftrightarrow x^2-\sqrt{x^3-x^2}-\sqrt{x^2-x}=0\)
=>\(\sqrt{x}\left(x\sqrt{x}-\sqrt{x^2-x}-\sqrt{x-1}\right)=0\)
=>căn x=0
=>x=0
















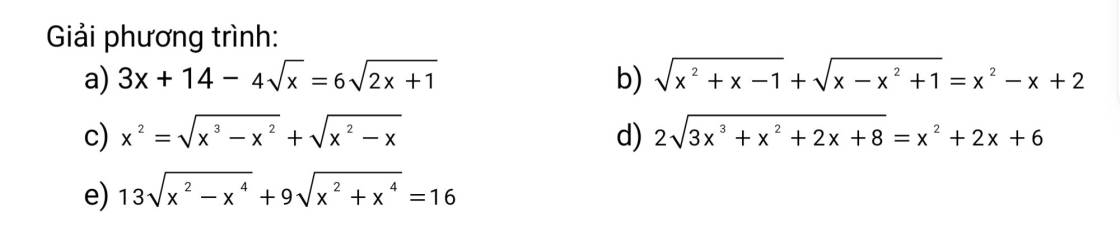 Nhờ mn giúp em vs ạ. c.ơn nhìu
Nhờ mn giúp em vs ạ. c.ơn nhìu