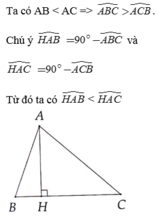
Cho ΔABC có ba góc nhọn, kẻ AH ⊥BC(H∈BC) có BH<HC. Chứng minh AB<AC bằng hai cách khác nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét ΔABC có BH<HC
mà AB là đường xiên của BH
và AC là đường xiên của CH
nên AB<AC

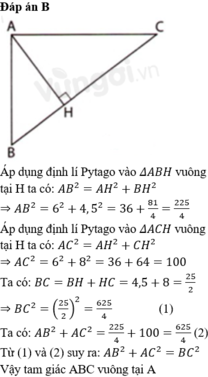
- Áp dụng định lý pi ta go vào tam giác ABC vuông tại A ta được :
\(AB^2+AC^2=BC^2\)
\(\Rightarrow AC^2+5^2=13^2\)
\(\Rightarrow AC=12\left(cm\right)\)
- Xét tam giác BHA và tam giác BAC có : \(\left\{{}\begin{matrix}\widehat{BHA}=\widehat{BAC}=90^o\\\widehat{B}\left(chung\right)\end{matrix}\right.\)
=> Hai tam giác trên đồng dạng .
=> \(\dfrac{BH}{AB}=\dfrac{AB}{BC}\)
=> \(BH=\dfrac{AB^2}{BC}=\dfrac{25}{13}\left(cm\right)\)
=> \(CH=BC-BH=\dfrac{144}{13}\left(cm\right)\)
- Áp dụng định lý pi ta go vào tam giác ABH vuông tại H ta được :
\(AH^2+BH^2=AB^2\)
\(\Rightarrow AH=\dfrac{60}{13}\left(cm\right)\)
Vậy ...

Bài 2:
b: \(AH\cdot\left(\cot\widehat{B}+\cot\widehat{C}\right)\)
\(=AH\cdot\left(\dfrac{BH}{AH}+\dfrac{CH}{AH}\right)\)
\(=AH\cdot\dfrac{BC}{AH}=BC\)

Theo định lí Pytago tam giác AHC vuông tại H
\(HC=\sqrt{AC^2-AH^2}=16cm\)
Theo định lí Ptago tam giác AHB vuông tại H
\(AB=\sqrt{AH^2+HB^2}=13cm\)
-> BC = HB + HC = 5 + 16 = 21 cm

a: ΔBHD vuông tại H
=>BH<BD
BH=BD khi H trùng với D
=>AD vuông góc BC
b: ΔCKD vuông tại K
=>CK<CD
mà BH<BD
nên BH+CK<BC

A B C H
a) Xét t/giác ABH vuông tại H , ta có: AB2 = AH2 + BH2 (Pi - ta - go)
=> AB2 = 122 + 52 = 169 => AB = 13 (cm)
Ta có: HC + BH = BC => HC = BC - BH = 14 - 5 = 9 (cm)
Xét t/giác AHC vuông tại H, có: AC2 = HC2 + AH2 (Pi - ta - go)
=> AC2 = 92 + 122 = 225 => AC = 15 (cm)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow AB^2=12^2+5^2=169\)
hay AB=13(cm)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên CH=BC-BH=14-5=9(cm)
Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow AC^2=12^2+9^2=225\)
hay AC=15(cm)
Vậy: AB=13cm; AC=15cm