Cho hình lục giác đều ABCDEF có tâm O.
a) Tìm các vectơ bằng vectơ OA, AB
b)Ngược hướng với OC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 9 2017
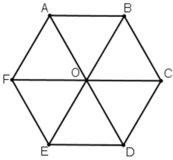
a) Các vectơ khác vectơ O→ và cùng phương với vectơ OA→ là:
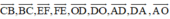
b) Các vectơ bằng vectơ AB→ là:
PT
1
CM
11 tháng 3 2017
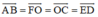
Do ABCDEF là lục giác đều tâm O nên AB = BC = CD= DE = EF = FA = OC.
Trên hình có tất cả 12 đoạn thẳng bằng nhau và bằng OC, tạo thành 24 vectơ có độ dài bằng OC. Trừ ra vectơ O C → còn lại 23 vectơ.
Chọn D.
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
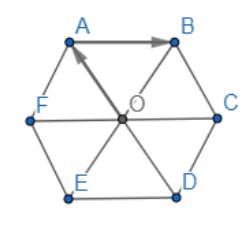
a) Ta có: AO // BC // EF
Suy ra các vectơ khác vectơ khác vectơ \(\overrightarrow 0 \) và cùng hướng với vectơ \(\overrightarrow {OA} \) là : \(\overrightarrow {DO} ,\overrightarrow {DA} ,\overrightarrow {CB} ,\overrightarrow {EF} \)
b) Ta có: \(OA = OB = OC = OD = OE = FO\) và AB // FC // ED
Suy ra các vectơ bằng vectơ \(\overrightarrow {AB} \) là \(\overrightarrow {FO} ,\overrightarrow {OC} ,\overrightarrow {ED} \)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
Chắc là lục giác đều?
Các vecto bằng \(\overrightarrow{AB}\) là \(\overrightarrow{FO};\overrightarrow{OC};\overrightarrow{ED}\)
PT
Cho lục giác đều ABCDEF tâm O. Số các vectơ khác O A → và cùng phương với nó là
A. 5
B. 6
C. 9
D. 10
1
CM
17 tháng 2 2017
Ta có: BC // AD // EF.
Do đó, các vectơ khác O A → và cùng phương với nó là:
B C → ; C B → ; O D → ; D O → ; A O → ; A D → ; D A → ; E F → ; F E →
Vậy số các vectơ khác O A → cùng phương với nó là 9 .
Chọn C.
BT
18 tháng 5 2017
Các véc tơ bằng véc tơ \(\overrightarrow{OC}\) có điểm đầu và điểm cuối là đỉnh lục giác là: \(\overrightarrow{FO};\overrightarrow{AB};\overrightarrow{ED}\).
Vậy có 3 véc tơ.
a: \(\overrightarrow{OA}=\overrightarrow{DO}=\overrightarrow{CB}=\overrightarrow{EF}\)
\(\overrightarrow{AB}=\overrightarrow{ED}=\overrightarrow{FO}=\overrightarrow{OC}\)