cho tam giác ABC, góc C =30o , B=45o , BC =8 cm. Tinh AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
5 tháng 7 2021
Ta có :
góc C = 180o - 105o - 30o = 45o
Kẻ đường cao AH
Gọi BH = x(cm) $\to$ CH = 2 - x(cm)
Trong tam giác AHB vuông tại H và tam giác AHC vuông tại H, ta có :
\(AH=BH.tanB=x.tan45^o=x\\ AH=CH.tanC=\left(2-x\right).tan30^o=\dfrac{\sqrt{3}}{3}\left(2-x\right)\)
Suy ra :
\(x=\dfrac{\sqrt{3}}{3}\left(2-x\right)\Leftrightarrow x=\dfrac{2\sqrt{3}}{3+\sqrt{3}}\)
Suy ra:
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.\dfrac{2\sqrt{3}}{3+\sqrt{3}}.2\simeq0,732\left(cm^2\right)\)
12 tháng 11 2023
Xét ΔABC có
\(cosC=\dfrac{CA^2+CB^2-AB^2}{2\cdot CA\cdot CB}\)
=>\(\dfrac{8^2+6^2-AB^2}{2\cdot6\cdot8}=cos30=\dfrac{\sqrt{3}}{2}\)
=>\(100-AB^2=48\sqrt{3}\)
=>\(AB=\sqrt{100-48\sqrt{3}}\simeq4,11\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot BA\cdot BC\cdot sinC\)
\(=\dfrac{1}{2}\cdot6\cdot8\cdot sin30=3\cdot8\cdot\dfrac{1}{2}=3\cdot4=12\)
12 tháng 11 2023
\(AB=\sqrt{AC^2+BC^2-2.AC.BC.cosC}\)
\(AB=4,11\)
\(S_{ABC}=\dfrac{1}{2}. AC.BC.sinC\)
\(S_{ABC}=\dfrac{1}{2}. 8.6.sin 30^o\)
\(S_{ABC}=12\)
4 tháng 7 2017
tự draw hình please !!! T ko biết vẽ trên máy thôg cảm
Vẽ đường cao AH của tam giác ABC
Ta có : \(AH\cdot BC=AB\cdot AC\)\(\Leftrightarrow AH=\frac{AB\cdot AC}{BC}=\frac{8\cdot12}{16}=6\left(cm\right)\)
Ta lại có :
\(\sin B=\frac{AH}{AB}=\frac{6}{8}\)\(\Rightarrow\widehat{B}\approx48^o35^'\)
\(\sin C=\frac{AH}{AC}=\frac{6}{12}\)\(\Rightarrow\widehat{C}=30^o\)
4 tháng 7 2017
Úi ! sai ùi tui đọc lộn đề đừng làm theo !!! SOrrrrryyyyyyyyyyyyyy
2 tháng 3 2022
Theo định lí Pytago tam giác ABC vuông tại A
\(AC=\sqrt{BC^2-AB^2}=6cm\)
Vì AC < AB => ^B < ^C
DN
3
5 tháng 2 2022
a: BC=10cm
C=AB+BC+AC=6+8+10=24(cm)
b: Xét ΔABD vuông tại A và ΔHBD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔABD=ΔHBD
c: Ta có: ΔABD=ΔHBD
nên DA=DH
mà DH<DC
nên DA<DC
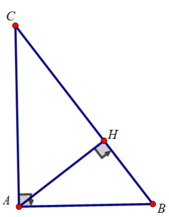
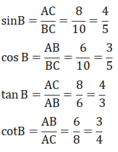
Từ A vẽ đường cao AH ta chứng minh được BH=AH=1/2AC
Đặt BH=a; HC=b =>a+b=8
Áp dụng định lý pytago vào tam giác AHC ta có được 3a^2=b^2
=>tìm được a = -4+4can3=>AB=\(\sqrt{2\left(64-32\sqrt{3}\right)}\)