Cho phương trình : 7x + y= \(\sqrt{2}\)(*)
a/ Cặp số ( 0;\(\sqrt{2}\)) có là nghiệm của phương trình (*) ko? Vì sao?
b/ Viết tập nghiệm của phương trình (*)
Giúp mình vs 😭
Ai nhanh và đúng nhất mình tích cho 😬
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 4 2022
\(\sqrt{7x+7}+\sqrt{7x-6}=t\ge0\)
\(bpt\Leftrightarrow t+t^2< 182\Leftrightarrow-14< t< 13\Leftrightarrow t< 13\Leftrightarrow\sqrt{7x+7}+\sqrt{7x-6}< 13\left(đk:x\ge\dfrac{6}{7}\right)\Leftrightarrow14x+1+2\sqrt{\left(7x+7\right)\left(7x-6\right)}< 169\Leftrightarrow2\sqrt{\left(7x+7\right)\left(7x-6\right)}< 168-14x\Leftrightarrow\left\{{}\begin{matrix}\left(7x+7\right)\left(7x-6\right)\ge0\\168-14x\ge0\\4\left(7x+7\right)\left(7x-6\right)< \left(168-14x\right)^2\end{matrix}\right.\)
\(giảibpt\Rightarrowđáp\) \(số\)
3 tháng 1 2021
Đặt \(\sqrt{\dfrac{4x+9}{28}}=y+\dfrac{1}{2}\left(y\ge-\dfrac{1}{2}\right)\).
Ta có hpt:
\(\left\{{}\begin{matrix}14y^2+14y=2x+1\\14x^2+14x=2y+1\end{matrix}\right.\)
\(\Rightarrow14\left(x^2-y^2\right)+16\left(x-y\right)=0\Leftrightarrow\left[{}\begin{matrix}x-y=0\\x+y=\dfrac{-8}{7}\end{matrix}\right.\).
Đến đây thế vào là được.
AH
Akai Haruma
Giáo viên
29 tháng 4 2023
Bài 1: ĐKXĐ: $2\leq x\leq 4$
PT $\Leftrightarrow (\sqrt{x-2}+\sqrt{4-x})^2=2$
$\Leftrightarrow 2+2\sqrt{(x-2)(4-x)}=2$
$\Leftrightarrow (x-2)(4-x)=0$
$\Leftrightarrow x-2=0$ hoặc $4-x=0$
$\Leftrightarrow x=2$ hoặc $x=4$ (tm)
AH
Akai Haruma
Giáo viên
29 tháng 4 2023
Bài 2:
PT $\Leftrightarrow 4x^3(x-1)-3x^2(x-1)+6x(x-1)-4(x-1)=0$
$\Leftrightarrow (x-1)(4x^3-3x^2+6x-4)=0$
$\Leftrightarrow x=1$ hoặc $4x^3-3x^2+6x-4=0$
Với $4x^3-3x^2+6x-4=0(*)$
Đặt $x=t+\frac{1}{4}$ thì pt $(*)$ trở thành:
$4t^3+\frac{21}{4}t-\frac{21}{8}=0$
Đặt $t=m-\frac{7}{16m}$ thì pt trở thành:
$4m^3-\frac{343}{1024m^3}-\frac{21}{8}=0$
$\Leftrightarrow 4096m^6-2688m^3-343=0$
Coi đây là pt bậc 2 ẩn $m^3$ và giải ta thu được \(m=\frac{\sqrt[3]{49}}{4}\) hoặc \(m=\frac{-\sqrt[3]{7}}{4}\)
Khi đó ta thu được \(x=\frac{1}{4}(1-\sqrt[3]{7}+\sqrt[3]{49})\)
LA
29 tháng 3 2022
1. 3x( x - 2 ) - ( x - 2 ) = 0
<=> ( x-2).(3x-1) = 0 => x = 2 hoặc x = \(\dfrac{1}{3}\)
2. x( x-1 ) ( x2 + x + 1 ) - 4( x - 1 )
<=> ( x - 1 ).( x (x^2 + x + 1 ) - 4 ) = 0
(phần này tui giải được x = 1 thôi còn bên kia giải ko ra nha )
3 \(\left\{{}\begin{matrix}\sqrt{5}x-2y=7\\\sqrt{5}x-5y=10\end{matrix}\right.\)<=> \(\left\{{}\begin{matrix}y=-1\\x=\sqrt{5}\end{matrix}\right.\)
AH
29 tháng 3 2022
\(1. 3x^2 - 7x +2=0\)
=>\(Δ=(-7)^2 - 4.3.2\)
\(= 49-24 = 25\)
Vì 25>0 suy ra phương trình có 2 nghiệm phân biệt:
\(x_1\)=\(\dfrac{-\left(-7\right)+\sqrt{25}}{2.3}=\dfrac{7+5}{6}=2\)
\(x_2\)=\(\dfrac{-\left(-7\right)-\sqrt{25}}{2.3}=\dfrac{7-5}{6}=\dfrac{1}{3}\)
CM
12 tháng 1 2019
- Ta có:
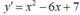
- Hệ số góc tiếp tuyến y'(0) = 7.
- Phương trình tiếp tuyến tại A(0 ; 2) là:
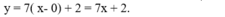
Chọn A.
10 tháng 9 2023
a) \(x^3-4x^2-5x+6=\sqrt[3]{7x^2+9x-4}\)
\(\Leftrightarrow-7x^2-9x+4+x^3+3x^2+4x+2=\sqrt[3]{7x^2+9x-4}\)
\(\Leftrightarrow-\left(7x^2+9x-4\right)+\left(x+1\right)^3+x+1=\sqrt[3]{7x^2+9x-4}\) (*)
Đặt \(\sqrt[3]{7x^2+9x-4}=a;x+1=b\)
Khi đó (*) \(\Leftrightarrow-a^3+b^3+b=a\)
\(\Leftrightarrow\left(b-a\right).\left(b^2+ab+a^2+1\right)=0\)
\(\Leftrightarrow b=a\)
Hay \(x+1=\sqrt[3]{7x^2+9x-4}\)
\(\Leftrightarrow\left(x+1\right)^3=7x^2+9x-4\)
\(\Leftrightarrow x^3-4x^2-6x+5=0\)
\(\Leftrightarrow x^3-4x^2-5x-x+5=0\)
\(\Leftrightarrow\left(x-5\right)\left(x^2+x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{-1\pm\sqrt{5}}{2}\end{matrix}\right.\)
MH
Chứng minh rằng tồn tại một cặp số duy nhất (x, y) thỏa mãn phương trình:
\(x^2-4x+y-6\sqrt{y}+13=0\)
3
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 4 2021
Đề bài sai
Chỉ tồn tại duy nhất cặp x;y thỏa mãn pt khi đề bài là:
\(x^2-4x+y-6\sqrt{y}+13=0\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 4 2021
ĐKXĐ: ...
\(\Leftrightarrow\left(x^2-4x+4\right)+\left(y-6\sqrt{y}+9\right)=0\)
\(\Leftrightarrow\left(x-2\right)^2+\left(\sqrt{y}-3\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2=0\\\sqrt{y}-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=9\end{matrix}\right.\)
Vậy có duy nhất cặp số (x;y)=(2;9) thỏa mãn phương trình
14 tháng 3 2020
ĐK: \(x\ge1\)
Từ pt (1) <=> \(\left(y^2-y\sqrt{x-1}\right)-\left(y-\sqrt{x-1}\right)=0\)
<=> \(y\left(y-\sqrt{x-1}\right)-\left(y-\sqrt{x-1}\right)=0\)
<=> \(\left(y-1\right)\left(y-\sqrt{x-1}\right)=0\)
<=> \(\orbr{\begin{cases}y-1=0\\y-\sqrt{x-1}=0\end{cases}}\)
+) Với y - 1 =0 <=> y = 1 thay vào pt thứ 2 ta có:
\(x^2+1=\sqrt{7x^2-3}\)
<=> \(x^4-5x^2+4=0\)
<=> \(\orbr{\begin{cases}x^2=4\\x^2=1\end{cases}}\)<=> x = 2 (tm đk) ; x = -2 ( loại ); x = 1 ( tmđk ) ; x = -1 (loại)
=> Trường hợp này có 2 nghiệm: ( x ; y ) là ( 2; 1 ) và ( 1; 1 )
+) Với \(y-\sqrt{x-1}=0\)<=> \(y=\sqrt{x-1}\) thay vào pt (2) ta có:
\(x^2+\sqrt{x-1}-\sqrt{7x^2-3}=0\)
<=> \(\left(x^2-4\right)+\left(\sqrt{x-1}-1\right)-\left(\sqrt{7x^2-3}-5\right)=0\)
<=> \(\left(x-2\right)\left(x+2+\frac{1}{\sqrt{x-1}+1}-\frac{7\left(x+2\right)}{\sqrt{7x^2-3}+5}\right)=0\)
<=> \(\orbr{\begin{cases}x-2=0\\x+2+\frac{1}{\sqrt{x-1}+1}-\frac{7\left(x+2\right)}{\sqrt{7x^2-3}+5}=0\left(loai\right)\end{cases}}\)
( vì \(x+2+\frac{1}{\sqrt{x-1}+1}-\frac{7\left(x+2\right)}{\sqrt{7x^2-3}+5}=\left(x+2\right)\left(1-\frac{7}{\sqrt{7x^2-3}+5}\right)+\frac{1}{\sqrt{x-1}+1}>0\)
với mọi x > = 1 )
<=> x = 2 (tm)
Thay vào pt dưới ta có: y = 1
=> trường hợp này có nghiệm ( 2; 1)
Kết luận:...