Câu hỏi : Tìm 4 số nguyên biết tổng ba trong bốn số lần lượt là 11 ; -21 ; 34 ; 0
GIÚP MÌNH VỚI , AI NHANH MÌNH K
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ dữ kiện thứ hai, ta thấy 4 số có cùng số dư khi chia cho 3 nên tổng nhỏ nhất là \(1+7+13+19=40\) (giữ lại đáp án ban đầu nhé)
Từ dữ kiện thứ nhất ta thấy hoặc cả 4 số đều lẻ, hoặc cả 4 số đều chẵn.
Từ dữ kiện thứ 2 ta thấy cả 4 số đều phải chia hết cho 3.
Suy ra tổng nhỏ nhất của 4 số là \(1+7+13+19=40\)

Bài 2:
Trường hợp 1: n=3
=>n+10=13 và n+14=17(nhận)
Trường hợp 2: n=3k+1
n+14=3k+15(loại)
Trường hợp 3: n=3k+2
n+10=3k+12(loại)
Vậy: n=3

Gọi 3 số lần lượt là n; n+1; n+2
3 tích lần lượt là:
\(n\left(n+1\right)=n^2+n\\ n\left(n+2\right)=n^2+2n\\ \left(n+1\right)\left(n+2\right)=n^2+3n+2\)
Theo đề bài, ta có:
\(n^2+n+n^2+2n+n^2+3n+2=242\\ \Leftrightarrow3n^2+6n-240=0\\ \Leftrightarrow3\left(n-8\right)\left(n+10\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}n=8\\n=-10\end{matrix}\right.\)
Vậy bộ 3 số đó là \(\left\{8;9;10\right\},\left\{-10;-9;-8\right\}\)

Gọi 3 số nguyên liến tiếp lần lượt là a ; a + 1 ; a + 2.
a(a + 1) + a(a + 2) + (a + 1)(a + 2) = 242
a2 + a + a2 + 2a + a2 + 3a + 2 = 242
3a2 + 6a + 2 = 242
3(a2 + 2a) = 242 - 2
a2 + 2a + 1 - 1 = 240 : 3
(a + 1)2 = 80 + 1
(a + 1)2 = 81
\(\left(a+1\right)^2=\left(\pm9\right)^2\)
\(a+1=\pm9\)
a + 1 = \(\pm9\)
a = \(\pm8\)
a + 2 = \(\pm10\)
Vậy 3 số nguyên đó là 8 ; 9 ; 10 hoặc - 8 ; - 9 ; - 10
Gọi 3 số nguyên liên tiếp cần tìm là: a; a + 1; a + 2
Các tích lập được thỏa mãn là: a.(a + 1); (a + 1).(a + 2); (a + 2).a
Ta có: a.(a + 1) + (a + 1).(a + 2) + (a + 2).a = 242
=> a2 + a + (a + 1).a + (a + 1).2 + a2 + 2a = 242
=> a2 + a + a2 + a + 2a + 2 + a2 + 2a = 242
=> 3a2 + 6a + 2 = 242
=> 3a.(a + 2) = 242 - 2 = 240
=> a.(a + 2) = 240 : 3 = 80
=> a.(a + 2) = 8.10 = -10.(-8)
=> a = 8 hoặc a = -10
Vậy 3 số nguyên liên tiếp cần tìm là: 8; 9; 10 hoặc -10; -9; -8

1. Ta có: trong 25 số nguyên tố có 1 số nguyên tố chẵn còn lại là 24 số nguyên tố lẻ. Tổng của 24 số lẻ là một số chẵn nên tổng của 25 số nguyên tố nhỏ hơn 100 là số chẵn.

Chọn B.
Gọi bốn số đó là a ;b ;c ;d ta có hệ:
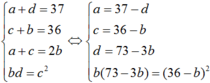
Giải ra ta được : b = 16 ; c = 20 ; d = 25 ; a = 12.