giúp e ạ
Chứng minh rằng qua ba điểm không thẳng hàng ta vẽ được một và chỉ mộtđường tròn. Với ba điểm thẳng hàng thì kết luận sẽ như thế nào? Vì sao?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Có năm đường thảng phân biệt trong hình vẽ, đó là: EA , EB , EC , ED , AB .
- Hai đường thẳng AB và CD trùng nhau; đường thẳng a song song với đường thẳng AB nên cũng song song với đường thẳng CD. Do đó, đường thẳng a không cắt đường thẳng CD.
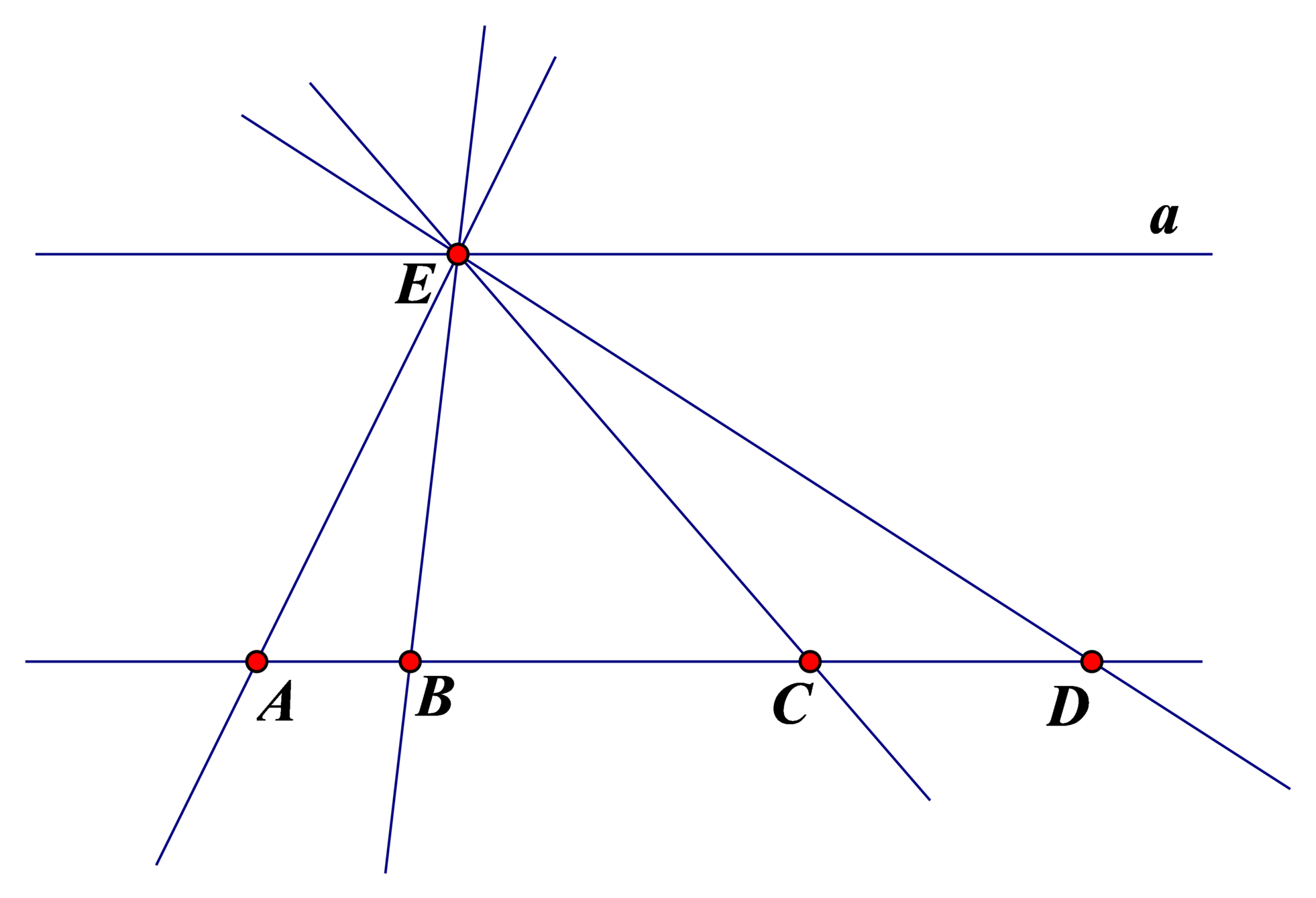

Câu b mk ko hiểu lắm với lại mk nhìn ko ra á bn,bn có thể nói lại dc ko

Giao điểm của AB và CD chính là điểm M thỏa mãn đề bài.
Một lẽ dĩ nhiên là nếu AB song song với CD thì ta không thể tìm được giao điểm của chúng, dẫn đến không tìm được điểm M theo yêu cầu.
Qua 3 điểm không thẳng hàng chỉ vẽ được một và chỉ một tam giác, từ đó suy ra chỉ vẽ được một và chỉ một đường tròn ngoại tiếp qua tam giác đó hay chỉ vẽ được một và chỉ một đường tròn đi qua 3 điểm không thẳng hàng
Với 3 điểm thẳng hàng thì sẽ không dựng được tam giác nên sẽ không vẽ được đường tròn đi qua 3 điểm đó
Với 3 điểm không thẳng hàng sẽ tạo ra được 1 tam giác . Bằng việc vẽ đường trung trực của 2 đoạn , ta sẽ tìn được tâm của tam giác đó ( đi qua 3 điểm không thẳng hàng )
Tương tự như vậy , nếu có 1 đường tròn đi qua 3 điểm thẳng hàng thì ta có thể xác định tâm của đường tròn đó bằng cách xđ giao điểm của 3 đường trung trực
Theo hình vẽ thì 2 đường trung trực song song vs nhau
=> Ko có đường tròn nào đi qua 3 điểm thẳng hàng