Làm hộ mình bài 3với 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1:
\(C=\dfrac{2}{1.4}+\dfrac{2}{4.7}+\dfrac{2}{7.10}+...+\dfrac{2}{97.100}\)
\(C=\dfrac{2}{3}.\left(\dfrac{3}{1.4}+\dfrac{3}{4.7}+\dfrac{3}{7.10}+...+\dfrac{3}{97.100}\right)\)
\(C=\dfrac{2}{3}.\left(\dfrac{1}{1}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{97}-\dfrac{1}{100}\right)\)
\(C=\dfrac{2}{3}.\left(\dfrac{1}{1}-\dfrac{1}{100}\right)\)
\(C=\dfrac{2}{3}.\dfrac{99}{100}\)
\(C=\dfrac{33}{50}\)
Câu 3:
a) Gọi ƯCLN(2n+5;n+3)=d
\(\Rightarrow\left\{{}\begin{matrix}2n+5⋮d\\n+3⋮d\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2n+5⋮d\\2.\left(n+3\right)⋮d\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2n+5⋮d\\2n+6⋮d\end{matrix}\right.\)
\(\Rightarrow\left(2n+6\right)-\left(2n+5\right)⋮d\)
\(\Rightarrow1⋮d\)
\(\Rightarrow d=1\)
Vậy \(\dfrac{2n+5}{n+3}\) là p/s tối giản
b) Để \(B=\dfrac{2n+5}{n+3}\) là số nguyên thì \(2n+5⋮n+3\)
\(2n+5⋮n+3\)
\(\Rightarrow2n+6-1⋮n+3\)
\(\Rightarrow1⋮n+3\)
\(\Rightarrow n+3\inƯ\left(1\right)=\left\{-1;1\right\}\)
Ta có bảng giá trị:
\(n+3=-1\rightarrow n=-4\)
\(n+3=1\rightarrow n=-2\)
Vậy \(n\in\left\{-4;-2\right\}\)

b: \(=8+2\cdot3-7\cdot1.3+3\cdot\dfrac{5}{4}=8.65\)

Phần 2: Tự luận
Câu 1:
1: Ta có: \(4\dfrac{1}{24}-\dfrac{35}{8}:\left(\dfrac{7}{4}-\dfrac{7}{12}\right)+\dfrac{1}{16}\cdot\dfrac{2}{3}\)
\(=\dfrac{97}{24}-\dfrac{35}{8}:\left(\dfrac{21}{12}-\dfrac{7}{12}\right)+\dfrac{1}{16}\cdot\dfrac{2}{3}\)
\(=\dfrac{97}{24}-\dfrac{35}{8}:\dfrac{14}{12}+\dfrac{1}{24}\)
\(=\dfrac{98}{24}-\dfrac{35}{8}\cdot\dfrac{6}{7}\)
\(=\dfrac{49}{12}-\dfrac{15}{4}\)
\(=\dfrac{49}{12}-\dfrac{45}{12}=\dfrac{4}{12}=\dfrac{1}{3}\)

Bài 4:
a) Vì $ABC$ cân tại $A$ nên $AB=AC$ và $\widehat{ABC}=\widehat{ACB}$
$\Rightarrow 180^0-\widehat{ABC}=180^0-\widehat{ACB}$
hay $\widehat{ABQ}=\widehat{ACR}$
Xét tam giác $ABQ$ và $ACR$ có:
$AB=AC$ (cmt)
$\widehat{ABQ}=\widehat{ACR}$ (cmt)
$BQ=CR$ (gt)
$\Rightarrow \triangle ABQ=\triangle ACR$ (c.g.c)
$\Rightarrow AQ=AR$
b)
$H$ là trung điểm của $BC$ nên $HB=HC$
Mà $QB=CR nên $HB+QB=HC+CR$ hay $QH=HR$
Xét tam giác $AQH$ và $ARH$ có:
$AQ=AR$ (cmt)
$QH=RH$ (cmt)
$AH$ chung
$\Rightarrow \triangle AQH=\triangle ARH$ (c.c.c)
$\Rightarrow \widehat{QAH}=\widehat{RAH}$


Câu 8
a, \(\dfrac{4}{5}+\dfrac{3}{8}+\dfrac{1}{4}=\dfrac{16.4}{80}+\dfrac{30}{80}+\dfrac{20}{80}=\dfrac{64+50}{80}=\dfrac{114}{80}=\dfrac{57}{40}\)
b, \(\dfrac{5}{9}+\dfrac{2}{3}+\dfrac{1}{2}=\dfrac{10}{18}+\dfrac{12}{18}+\dfrac{9}{18}=\dfrac{22+9}{18}=\dfrac{31}{18}\)



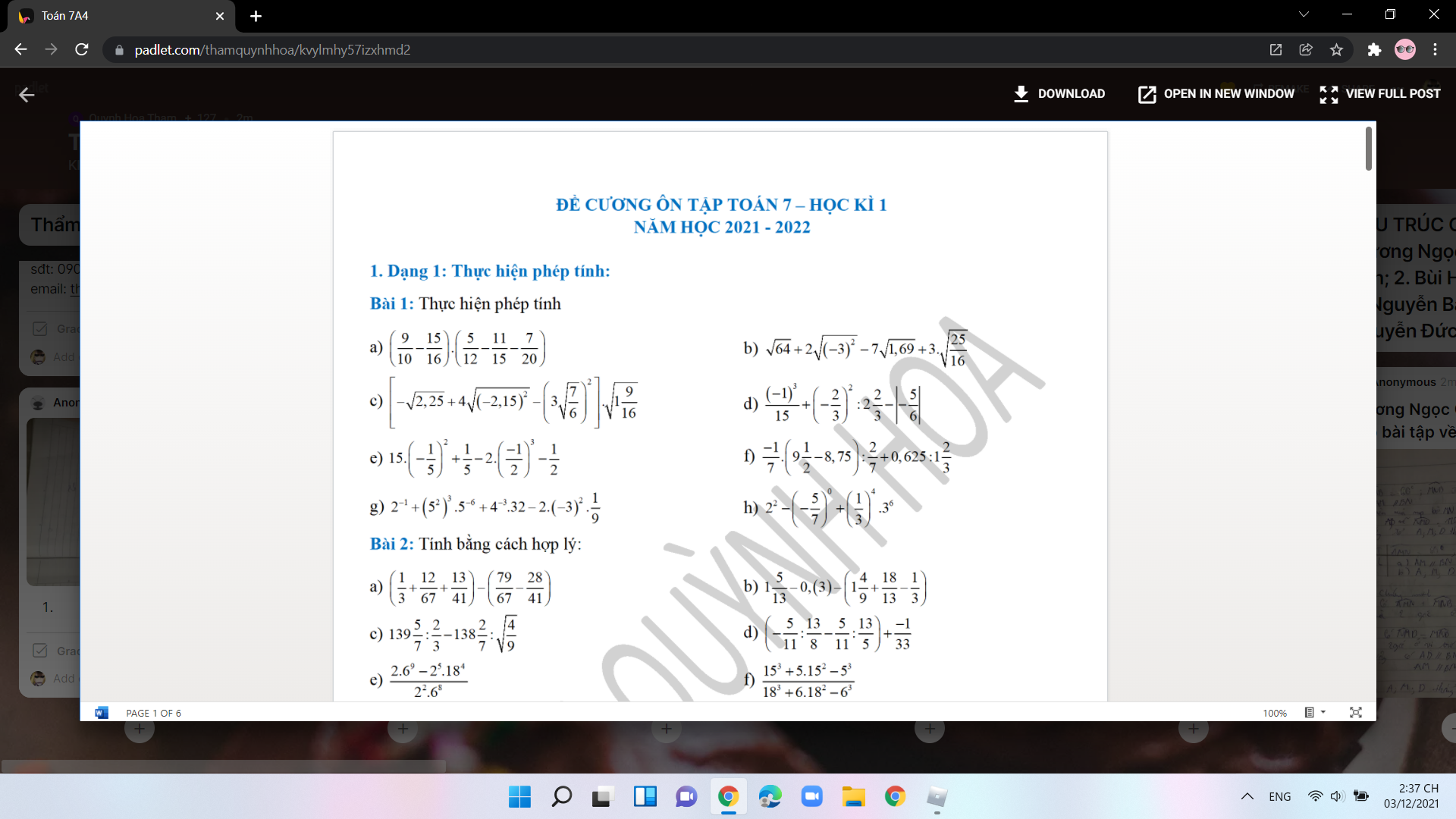 làm giúp mình bài 1 với, mình cần gấp ( nếu rảnh làm hộ mình bài 2 cũng dc )
làm giúp mình bài 1 với, mình cần gấp ( nếu rảnh làm hộ mình bài 2 cũng dc ) Làm hộ mình bài bán ý c) nhé
Làm hộ mình bài bán ý c) nhé Mọi người làm hộ mình bài 4,5,6 hộ mk cái nha...Mình cảm ơn các bạn rất nhiều
Mọi người làm hộ mình bài 4,5,6 hộ mk cái nha...Mình cảm ơn các bạn rất nhiều

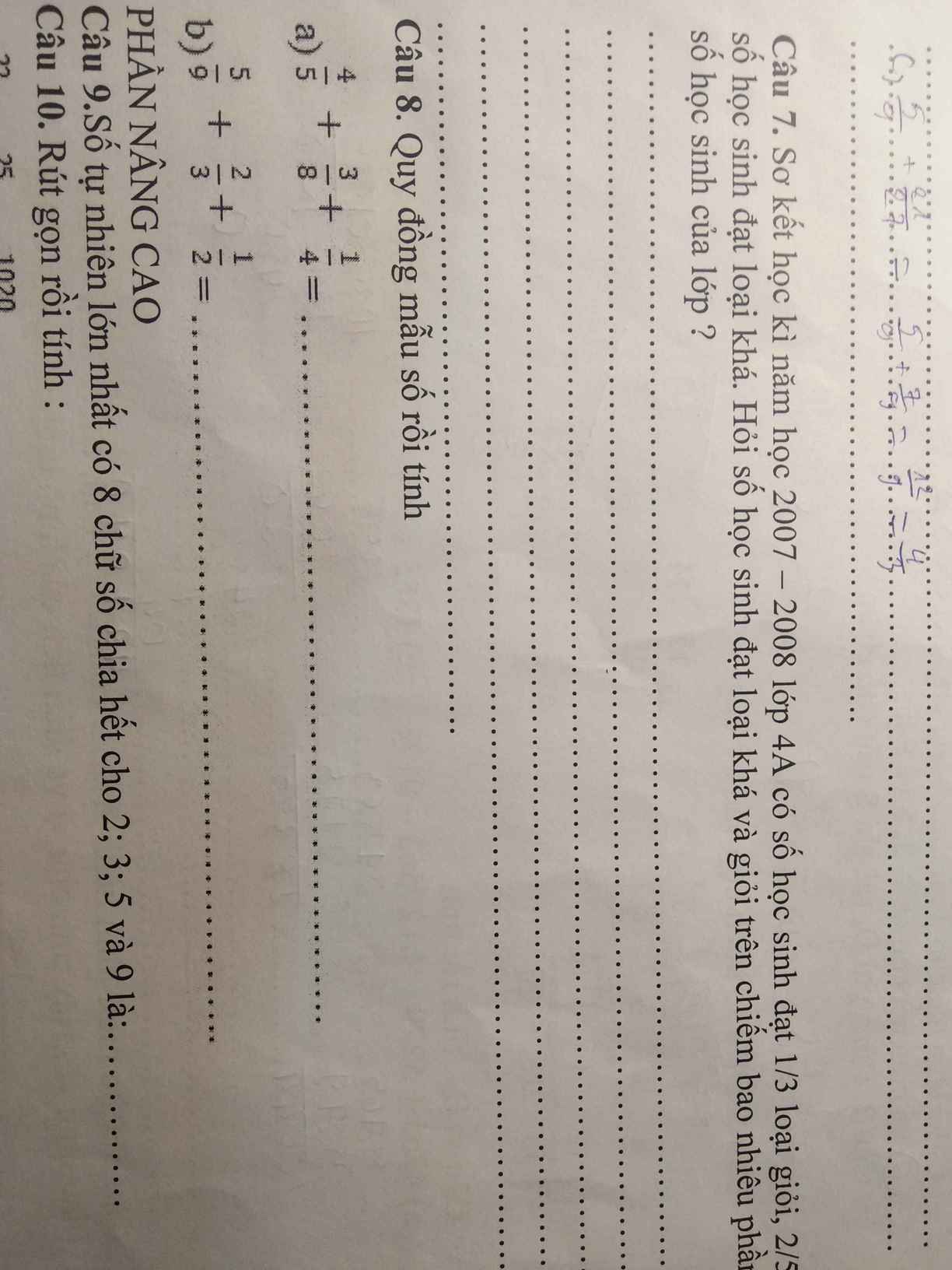
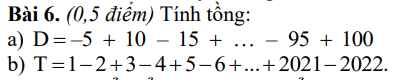
mk làm hộ bạn rồi mà
Làm rồi nhé bạn
Giúp mk làm tất bài này nhé - Hoc24