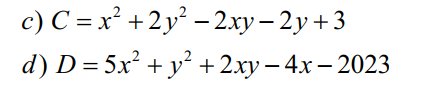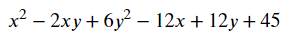Tìm GTNN của biểu thức; x2+y2-xy-2y-2x+2022.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KR
7 tháng 5 2018
Áp dụng Bunyakovsky, ta có :
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x.1+y.1\right)^2=1\)
=> \(\left(x^2+y^2\right)\ge\frac{1}{2}\)
=> \(Min_C=\frac{1}{2}\Leftrightarrow x=y=\frac{1}{2}\)
Mấy cái kia tương tự
PT
1
M
1
19 tháng 10 2021
\(A=\sqrt{x-1}+\sqrt{2}\ge\sqrt{2}\\ A_{max}=\sqrt{2}\Leftrightarrow x-1=0\Leftrightarrow x=1\)
19 tháng 10 2021
\(A=\sqrt{x-1}+\sqrt{2}\ge\sqrt{2}\forall x\)
Dấu '=' xảy ra khi x=1
HM
16 tháng 7 2023
c) C = x2 - 2xy+ y2 + y^2 - 2y +1 +2
= (x-y)^2 + (y - 1)^2 + 2
Ta có (x-y)^2;(y-1)^2 lớn hơn hoặc bằng 2
Dấu "=" xảy ra => (y-1)^2 = 0 => y-1=0 => y = 1
(x-y)^2 = 0 => x - y = 0 => x - 1= 0 => x = 1
d) D = \(4x^2-4x+1+x^2+2xy+y^2-2024\)
= \(\left(2x-1\right)^2+\left(x+y\right)^2-2024\)
Ta có (2x-1)^2;(x+y)^2 ≥ 0 => D ≥ -2024
Dấu = xảy ra => (2x-1)^2 = 0 => 2x-1 = 0 => x = 1/2
=> (x+y)^2 =0 => x+y=0 => 1/2+y =0 => y = -1/2
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 1
\(=\left(x^2-2xy+y^2\right)-12\left(x-y\right)+36+5y^2+9\)
\(=\left(x-y\right)^2-12\left(x-y\right)+36+3y^2+9\)
\(=\left(x-y-6\right)^2+5y^2+9\ge9\)
Vậy GTNN của biểu thức là 9, xảy ra khi \(x=6;y=0\)